|
ΠΟΛΥΩΡΟΦΟΥ ΧΩΡΙΚΟΥ ΠΛΑΙΣΙΟΥ ΓΕΝΙΚΗ ΠΕΡΙΠΤΩΣΗ Δ.1 Περιγραφή του θέματος Η αξιολόγηση της λειτουργίας των μονώροφων επίπεδων πλαισίων σε οριζόντιες σεισμικές δυνάμεις, αναπτύχθηκε στην παράγραφο 5.1, όπου η στατική μονάδα που εξεταζόταν ήταν η κολόνα (υποστύλωμα ή τοιχίο). Στο παράρτημα Β εξετάστηκε η λειτουργία του πολυώροφου επίπεδου πλαισίου με στατική μονάδα το ζύγωμα. Στο κεφάλαιο αυτό εξετάζεται η σύνθεση των πλαισίων στο χώρο, η οποία γίνεται μέσω των δοκών και των πλακών. Η στατική μονάδα αξιολόγησης των συζευγμένων χωρικών πλαισίων είναι το διάφραγμα. Για να είναι εύκολη η παρακολούθηση αυτού του κεφαλαίου είναι χρήσιμο να έχει μελετηθεί πρώτα η παράγραφος 5.4, το Παράρτημα Β και το Παράρτημα Γ. 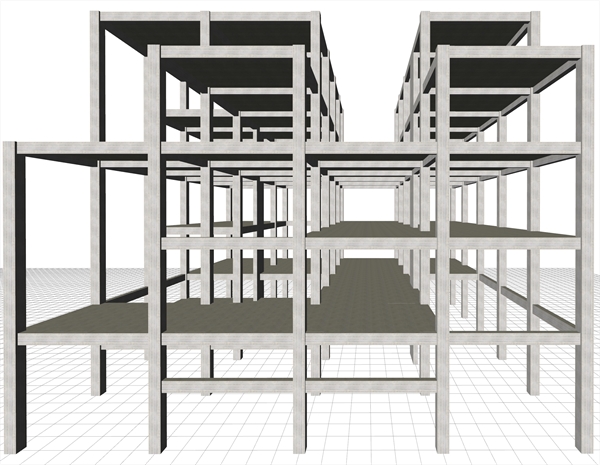 Εικόνα Δ.1-1: Ο σκελετός του κτιρίου με τις 6 στάθμες, μελέτη <B_d1>
Εικόνα Δ.1-1: Ο σκελετός του κτιρίου με τις 6 στάθμες, μελέτη <B_d1> Εικόνα Δ.1-1: Ο σκελετός του κτιρίου με τις 6 στάθμες, μελέτη <B_d1>
Διάφραγμα είναι το επίπεδο τμήμα του ορόφου που αποτελείται από πλάκες, οι οποίες συνδέουν δοκούς και κολόνες μεταξύ τους. Σε έναν όροφο μπορεί να υπάρχουν περισσότερα του ενός διαφράγματα, όπως φαίνεται στο κτίριο του παραδείγματος αυτής της παραγράφου. 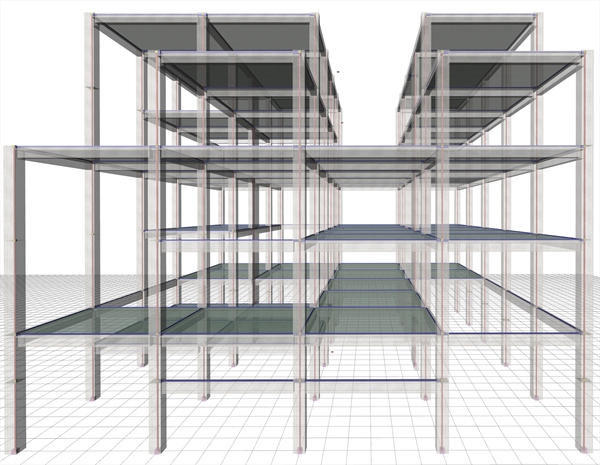 Εικόνα Δ.1-2: Το χωρικό προσομοίωμα του σκελετού του κτιρίου με τις ράβδους δοκών και κολονών και τα διαφράγματα
Εικόνα Δ.1-2: Το χωρικό προσομοίωμα του σκελετού του κτιρίου με τις ράβδους δοκών και κολονών και τα διαφράγματα Εικόνα Δ.1-2: Το χωρικό προσομοίωμα του σκελετού του κτιρίου με τις ράβδους δοκών και κολονών και τα διαφράγματα
Το πιο χαρακτηριστικό σημείο του διαφράγματος είναι το κέντρο ελαστικής στροφής το οποίο έχει περιγραφεί στις παραγράφους 3.1.4, 5.4.3.4 και Γ.5. Κέντρο ελαστικής στροφής CT διαφράγματος συγκεκριμένου ορόφου, είναι το σημείο στο επίπεδο του διαφράγματος, πέριξ του οποίου στρέφεται το διάφραγμα, όταν ασκηθεί επί αυτού μία οριζόντια σεισμική δύναμη H. Το σημείο CT είναι γεωμετρικό αποκλειστικά σημείο και δεν εξαρτάται από τη φόρτιση. Αυτό σημαίνει ότι είτε η οριζόντια σεισμική δύναμη είναι 2H, είτε 3H, είτε λάβει οποιαδήποτε άλλη τιμή, το κέντρο ελαστικής στροφής παραμένει το ίδιο. Βέβαια, εξαρτάται από τη γεωμετρία των υποκείμενων και των υπερκείμενων ορόφων. Κύριο σύστημα αξόνων διαφράγματος είναι το ορθογωνικό σύστημα αξόνων xCTy, στο οποίο όταν ασκηθεί οριζόντια σεισμική δύναμη H επί του CT, κατά τη διεύθυνση x (ή y), δίνει μετατόπιση του CT μόνο κατάx (ή y αντίστοιχα). Η γωνία a του κύριου συστήματος, ως προς το αρχικό σύστημα X0Y, ονομάζεται κύρια γωνία του διαφράγματος. Τα παραπάνω στοιχεία του διαφράγματος καθώς και η δυστρεψία Kθ και η έλλειψη δυστρεψίας (CT, rx, ry), πρέπει να υπολογιστούν με γενικό τρόπο. Η μέθοδος που θα χρησιμοποιηθεί θα πρέπει να μπορεί να αντιμετωπίσει ένα ή περισσότερα του ενός διαφράγματα στον όροφο. Επίσης πρέπει η γενική λύση να μπορεί να λαμβάνει υπόψη την επιρροή μη διαφραγματικών πλαισίων, όπως επίσης και την επιρροή της θεμελίωσης, η οποία μπορεί να βρίσκεται σε διαφορετικές στάθμες ορόφων. Το παράδειγμα που χρησιμοποιείται σ’ αυτήν την παράγραφο περιέχει τις περισσότερες ιδιαιτερότητες που μπορεί να εμφανιστούν στην πράξη, εκτός από τις θεμελιώσεις, αποκλειστικά και μόνο για λόγους απλοποίησης. Την πλήρη επίλυση (συμπεριλαμβανομένης της θεμελίωσης), μπορεί να πραγματοποιήσει ο μηχανικός με το συνοδευτικό λογισμικό. 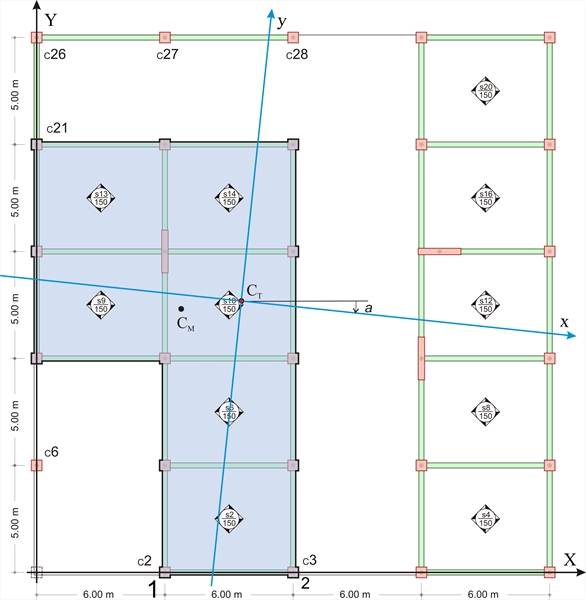 Εικόνα Δ.1-3: Η κάτοψη της 5ης στάθμης και το αριστερά διάφραγμα που θα εξετασθεί στη συνέχεια. Οι κολόνες έχουν διατομή 500/500, τα τοιχία 2000/300 και οι δοκοί 300/500.
Εικόνα Δ.1-3: Η κάτοψη της 5ης στάθμης και το αριστερά διάφραγμα που θα εξετασθεί στη συνέχεια. Οι κολόνες έχουν διατομή 500/500, τα τοιχία 2000/300 και οι δοκοί 300/500. Εικόνα Δ.1-3: Η κάτοψη της 5ης στάθμης και το αριστερά διάφραγμα που θα εξετασθεί στη συνέχεια. Οι κολόνες έχουν διατομή 500/500, τα τοιχία 2000/300 και οι δοκοί 300/500.
Η συμπεριφορά του αριστερά διαφράγματος της 5ης στάθμης που επιλύεται στη συνέχεια, επηρεάζεται άμεσα από το γάμα πλαίσιο C21-C 26-C27-C28 με το οποίο βρίσκεται σε επαφή, ενώ η κολόνα C6 καθώς και το δεξιό διάφραγμα, την επηρεάζουν έμμεσα, μέσω των πλαισίων των άλλων ορόφων. Στη συνέχεια αναπτύσσεται μια γενική μέθοδος προσδιορισμού των ζητούμενων στοιχείων του διαφράγματος. Η μέθοδος δημιουργεί μία κατάσταση στην οποία έχουμε μόνο στροφή στο διάφραγμα γύρω από το κέντρο ελαστικής στροφής CT, το οποίο παραμένει ακίνητο ως προς το έδαφος. Η μέθοδος αποτελείται από 4 βήματα, εκ των οποίων τα τρία πρώτα είναι από μία χωρική επίλυση.
Δ.2 Γενική μέθοδος υπολογισμού στοιχείων διαφράγματος i 1ο Βήμα : Επίλυση του φορέα με δύναμη HΧ και συγκεντρωμένη ροπή MCM,X στο κέντρο μάζας του διαφράγματος i. .jpg?bhow=0&w=600&h=600&Str=0) Εικόνα Δ.2-1: Φόρτιση: HX=100 και ροπή MCM,X επί του Κέντρου Μάζας CM του διαφράγματος i. Αποτελέσματα: οι συνολικές παραμορφώσεις του φορέα και οι μετακινήσεις του διαφράγματος i
Εικόνα Δ.2-1: Φόρτιση: HX=100 και ροπή MCM,X επί του Κέντρου Μάζας CM του διαφράγματος i. Αποτελέσματα: οι συνολικές παραμορφώσεις του φορέα και οι μετακινήσεις του διαφράγματος i Εικόνα Δ.2-1: Φόρτιση: HX=100 και ροπή MCM,X επί του Κέντρου Μάζας CM του διαφράγματος i. Αποτελέσματα: οι συνολικές παραμορφώσεις του φορέα και οι μετακινήσεις του διαφράγματος i
Χρειάζονται οι 2 μετακινήσεις δXX1, δXY1 του σημείου 1 του διαφράγματος i και η γωνία θXZ του διαφράγματος. Η τιμή της δύναμης HΧ στο παράδειγμα έχει δοθεί =100 kN. Η τιμή αυτή θα μπορούσε να είναι οποιαδήποτε, αρκεί να είναι ίδια και στις τρεις επιλύσεις των 3 πρώτων βημάτων. Η θέση άσκησης της δύναμης Hδεν παίζει ρόλο, είναι όμως πρακτικό να δίνουμε στη δύναμη μία τυχούσα εκκεντρότητα ως προς το κέντρο μάζας cy π.χ. 2.0 m, ώστε να προκύπτει σημαντική στροφή στο διάφραγμα, με συνέπεια μεγαλύτερη ακρίβεια στους υπολογισμούς. Η εκκεντρότητα αυτή είναι απαραίτητη, ιδιαίτερα στην περίπτωση που το κέντρο ελαστικήςστροφής είναι κοντά, ή συμπίπτει με το κέντρο μάζας. Επομένως, εκτός από τη δύναμηHΧ ασκούμε στο σημείο CM και ροπή MCM,x=100 kN·2.00m= 200 kNm. Αναγκαίο επίσης είναι η δύναμη H να έχει αρκετά μεγάλο μέγεθος, με συνέπεια να προκύπτουν ικανές μετατοπίσεις στο διάφραγμα, ώστε να μπορούν να ξεχωρίσουν από τις μετακινήσεις λόγω ροπής. Η έλλειψη δύναμης H και η εξάσκηση μόνο ροπής στο διάφραγμα δίνει στροφή, αλλά και μετακινήσεις, οι οποίες όμως δε μπορούν να υπολογιστούν αφού δεν είναι γνωστό ακόμη το κέντρο ελαστικής στροφής. Το σημείο 1 αντιστοιχεί στον κόμβο της κολόνας Κ2, μπορεί όμως να είναι ένα οποιοδήποτε σημείο του διαφράγματος. .jpg?bhow=0&w=600&h=600&Str=0) Εικόνα Δ.2-2: Οι μετακινήσεις του διαφράγματος σε κάτοψη, λόγω 2 παράλληλων μετατοπίσεων δXXo, δXYo και μίας στροφής θXZ
Εικόνα Δ.2-2: Οι μετακινήσεις του διαφράγματος σε κάτοψη, λόγω 2 παράλληλων μετατοπίσεων δXXo, δXYo και μίας στροφής θXZ Εικόνα Δ.2-2: Οι μετακινήσεις του διαφράγματος σε κάτοψη, λόγω 2 παράλληλων μετατοπίσεων δXXo, δXYo και μίας στροφής θXZ
Τα μόνα αποτελέσματα που χρειάζονται από αυτήν την επίλυση είναι οι μετατοπίσεις του σημείου 1 δXX1=2.681 mm, δXY1=-0.231 mm και η γωνία θ XZ=4.5613·10-5 του διαφράγματος. Οι μετακινήσεις του σημείου 2 θα χρησιμοποιηθούν μόνο για επιβεβαίωση της γενικότητας της μεθόδου. Όλες οι μετακινήσεις είναι απόλυτες ως προς το έδαφος. 2ο Βήμα: Επίλυση του φορέα με φόρτιση HΧ στο κέντρο μάζας του διαφράγματος i και δεσμευμένη τη γωνία στροφής του. .jpg?bhow=0&w=600&h=600&Str=0) Εικόνα Δ.2-3: Φόρτιση: Hx=100 επί του διαφράγματος i το οποίο είναι δεσμευμένο σε στροφή. Αποτελέσματα: οι συνολικές παραμορφώσεις του φορέα είναι οι δύο παράλληλες μετακινήσεις του διαφράγματος
Εικόνα Δ.2-3: Φόρτιση: Hx=100 επί του διαφράγματος i το οποίο είναι δεσμευμένο σε στροφή. Αποτελέσματα: οι συνολικές παραμορφώσεις του φορέα είναι οι δύο παράλληλες μετακινήσεις του διαφράγματος Εικόνα Δ.2-3: Φόρτιση: Hx=100 επί του διαφράγματος i το οποίο είναι δεσμευμένο σε στροφή. Αποτελέσματα: οι συνολικές παραμορφώσεις του φορέα είναι οι δύο παράλληλες μετακινήσεις του διαφράγματος
Αποτελέσματα: οι συνολικές παραμορφώσεις του φορέα είναι οι δύο παράλληλες μετακινήσεις του διαφράγματος Χρειαζόμαστε μόνο τις δύο μετακινήσεις του σημείου 1 δXXo, δXYo, οι οποίες είναι ίδιες για κάθε σημείο του διαφράγματος i, άρα και του σημείου CT, δεδομένου ότι η γωνία στροφής του διαφράγματος είναι μηδενική.
.jpg?bhow=0&w=600&h=600&Str=0) Εικόνα Δ.2-4: Οι 2 παράλληλες μετατοπίσεις δXXo, δXYo του διαφράγματος σε κάτοψη.Όλα τα σημεία του διαφράγματος, άρα και το CT, έχουν ίδιες μετατοπίσεις.Η στροφή του διαφράγματος είναι δεσμευμένη, γι’ αυτό θXZ=0.
Εικόνα Δ.2-4: Οι 2 παράλληλες μετατοπίσεις δXXo, δXYo του διαφράγματος σε κάτοψη.Όλα τα σημεία του διαφράγματος, άρα και το CT, έχουν ίδιες μετατοπίσεις.Η στροφή του διαφράγματος είναι δεσμευμένη, γι’ αυτό θXZ=0. Εικόνα Δ.2-4: Οι 2 παράλληλες μετατοπίσεις δXXo, δXYo του διαφράγματος σε κάτοψη.Όλα τα σημεία του διαφράγματος, άρα και το CT, έχουν ίδιες μετατοπίσεις.Η στροφή του διαφράγματος είναι δεσμευμένη, γι’ αυτό θXZ=0.
Όλα τα σημεία του διαφράγματος, άρα και το CT, έχουν ίδιες μετατοπίσεις. Η στροφή του διαφράγματος είναι δεσμευμένη, γι’ αυτό θXZ=0. Το διάφραγμα i, έχει μηδενική γωνία στροφής, γι’ αυτό το σημείο 1 έχει μόνο δύο παράλληλες μετατοπίσεις, δXXo =2.103 mm και δXYo=-0.047mm, οι οποίες είναι ίδιες σε όλα τα σημεία του διαφράγματος, άρα και στο σημείο CT. Στα άλλα συνεπίπεδα, υπερκείμενα και υποκείμενα διαφράγματα, υπάρχουν στροφές, μικρές μεν, αλλά υπολογίσιμες, γι’ αυτό και κάθε σημείο επί αυτών των διαφραγμάτων έχει διαφορετικές μετακινήσεις.
3ο Βήμα: Επίλυση του φορέα με φόρτιση HΥ στο κέντρο μάζας του διαφράγματος i, με δεσμευμένη τη γωνία στροφής του διαφράγματος i (μόνο) .jpg?bhow=0&w=600&h=600&Str=0) Εικόνα Δ.2-5: Φόρτιση: HY=100 επί του διαφράγματος i το οποίο είναι δεσμευμένο σε στροφή.
Εικόνα Δ.2-5: Φόρτιση: HY=100 επί του διαφράγματος i το οποίο είναι δεσμευμένο σε στροφή.
Αποτελέσματα: οι συνολικές παραμορφώσεις του φορέα είναι οι δύο παράλληλες μετακινήσεις του διαφράγματος Εικόνα Δ.2-5: Φόρτιση: HY=100 επί του διαφράγματος i το οποίο είναι δεσμευμένο σε στροφή.
Αποτελέσματα: οι συνολικές παραμορφώσεις του φορέα είναι οι δύο παράλληλες μετακινήσεις του διαφράγματος
Αποτελέσματα: οι συνολικές παραμορφώσεις του φορέα είναι οι δύο παράλληλες μετακινήσεις του διαφράγματος Χρειαζόμαστε μόνο τις δύο μετακινήσεις του σημείου 1 δΥXo, δΥYo που είναι οι δύο μετακινήσεις κάθε σημείου του διαφράγματος i, άρα και του σημείου CT, δεδομένου ότι η γωνία στροφής του διαφράγματος είναι μηδενική.
.jpg?bhow=0&w=600&h=600&Str=0) Εικόνα Δ.2-6: Οι 2 παράλληλες μετατοπίσεις δYXo, δYYo του διαφράγματος σε κάτοψη.
Εικόνα Δ.2-6: Οι 2 παράλληλες μετατοπίσεις δYXo, δYYo του διαφράγματος σε κάτοψη.
Όλα τα σημεία του διαφράγματος, άρα και το CT, έχουν αυτές τις δύο μετατοπίσεις.
Η στροφή του διαφράγματος είναι δεσμευμένη, γι’ αυτό θXZ=0. Εικόνα Δ.2-6: Οι 2 παράλληλες μετατοπίσεις δYXo, δYYo του διαφράγματος σε κάτοψη.
Όλα τα σημεία του διαφράγματος, άρα και το CT, έχουν αυτές τις δύο μετατοπίσεις.
Η στροφή του διαφράγματος είναι δεσμευμένη, γι’ αυτό θXZ=0.
Όλα τα σημεία του διαφράγματος, άρα και το CT, έχουν αυτές τις δύο μετατοπίσεις. Η στροφή του διαφράγματος είναι δεσμευμένη, γι’ αυτό θXZ=0. Το διάφραγμα i, έχει μηδενική γωνία στροφής, γι’ αυτό το σημείο 1 έχει μόνο δύο παράλληλες μετατοπίσεις, δYXo =-0.047 mm και δYYo=1.668 mm, οι οποίες είναι ίδιες σε όλα τα σημεία του διαφράγματος, άρα και στο σημείο CT. Όπως συνέβαινε στο 2ο βήμα, το ίδιο και σ’ αυτή τη φόρτιση, στα άλλα συνεπίπεδα, υπερκείμενα και υποκείμενα διαφράγματα, υπάρχουν στροφές, μικρές μεν, αλλά υπολογίσιμες, γι’ αυτό και κάθε σημείο επί αυτών των διαφραγμάτων έχει διαφορετικές μετακινήσεις. Οι δευτερεύουσες μετακινήσεις δXYo της 2ης και δYXo της 3ης φόρτισηςείναι πάντοτε ίσες μεταξύ τους, δηλαδή πρέπει πάντοτε από τη χωρική επίλυση να προκύπτουν δXYo=δ YXo. Η 3η επίλυση γίνεται μόνο για τον υπολογισμό της μετακίνησης δYYo που είναι αναγκαία για τον υπολογισμό της γωνίας a του κυρίου συστήματος. Από τα αποτελέσματα επομένως της 2ης και της 3ης επίλυσης προκύπτει η γωνία a του κυρίου συστήματος του διαφράγματος i από την εξίσωση Γ.9.1 της §Γ.9: tan(2a)=2 δ XYo /( δ XXo - δ YYo )=2 ·(-0.047)/(2.103-1.668)=-0216 → 2a=-12.2º → a=-6.1º 4ο Βήμα : Αποτελέσματα 1ης φόρτισης μείον 2ης φόρτισης, που σημαίνει ότι υπάρχει μόνο ροπή και μόνο στροφή γύρω από το κέντρο ελαστικής στροφής CT, το οποίο παραμένει σταθερό ως προς το έδαφος. .jpg?bhow=0&w=600&h=600&Str=0) Εικόνα Δ.2-7: Το μόνο φορτίο επί του διαφράγματος i είναι η ροπή επί του CT
Εικόνα Δ.2-7: Το μόνο φορτίο επί του διαφράγματος i είναι η ροπή επί του CT
Οι μετακινήσεις του διαφράγματος οφείλονται μόνο στη στροφή
Το κέντρο ελαστικής στροφής CT παραμένει ακίνητο ως προς το έδαφος Εικόνα Δ.2-7: Το μόνο φορτίο επί του διαφράγματος i είναι η ροπή επί του CT
Οι μετακινήσεις του διαφράγματος οφείλονται μόνο στη στροφή
Το κέντρο ελαστικής στροφής CT παραμένει ακίνητο ως προς το έδαφος
Οι μετακινήσεις του διαφράγματος οφείλονται μόνο στη στροφή Το κέντρο ελαστικής στροφής CT παραμένει ακίνητο ως προς το έδαφος Με το τέχνασμα που έχει χρησιμοποιηθεί, η αφαίρεση της 2ης από την 1η επίλυση δίνει μία κατάσταση μετακινήσεων στο φορέα όπου το διάφραγμα i έχει μόνο στροφή, ενώ όλα τα υπόλοιπα διαφράγματα έχουν εκτός από στροφή και μετακινήσεις. Αυτό που μας απασχολεί όμως είναι μόνο τοδιάφραγμα i. Το πιο σημαντικό αποτέλεσμα του τεχνάσματος είναι ότι η στροφή αυτή του διαφράγματος γίνεται γύρω από το κέντρο ελαστικής στροφής C T, το οποίο παραμένει ακίνητο ως προς το έδαφος, γεγονός που μας επιτρέπει να υπολογίσουμε την ακριβή του θέση. Η γωνία στροφής του διαφράγματος i είναι η γωνία στροφής θXZ που προσδιορίστηκε στο 1ο βήμα από την 1η φόρτιση.
.jpg?bhow=0&w=600&h=600&Str=0) Εικόνα Δ.2-8
Εικόνα Δ.2-8 Εικόνα Δ.2-8
Οι μετακινήσεις τυχόντος σημείου j του διαφράγματος, λόγω στροφής θXZ προκύπτουν από τις σχέσεις: δΧ tj =δ XXj -δ XXo , δ Ytj =δ XYj -δ XYo και οι συντεταγμένες του κέντρου ελαστικής στροφής CT που αντιστοιχούν σ’ αυτές τις μετακινήσεις (βλέπε §Γ.5): Στο συγκεκριμένο παράδειγμα, για το σημείο 1 προκύπτουν: δΧ t 1 =δ XX 1 -δ XXo =2.681-2.103=0.578 mm δ Yt 1 =δ XY 1 -δ XYo =-0.211-(-0.047)=-0.164 mm Η στροφή του διαφράγματος είναι ίδια με τη στροφή της 1ης επίλυσης, δηλαδή θXZ= 4.5613·10-5. Tο σημείο 1 έχει συντεταγμένες (6.0, 0.0) οπότε: XCT = X 1 -δ Yt 1 /θ XZ =6.0-(-0.164) ·10-3/(4.5613·10-5)=9.6 m YCT = Y 1 +δ Xt 1 /θ XZ =0.0+0.578 ·10-3/(4.5613·10-5)=12.7 m Παρατήρηση: Για επιβεβαίωση της γενικότητας της μεθόδου, υπολογίζουμε τις συντεταγμένες του CT και από το σημείο 2 (12.0, 0.0): δΧt2=δXX2-δXXo=2.681-2.103=0.578 mm δYt2=δXY2-δXYo=0.063-(-0.047)=0.110 mm XCT=X2-δYt2/θXZ=12.0-0.110·10-3/(4.5613·10-5)=9.6 m YCT=Y2+δXt2/θXZ=0.0+0.578·10-3/(4.5613·10-5)=12.7 m Με τον ίδιο τρόπο μπορούν να επαληθευτούν οι συντεταγμένες του CT από οποιοδήποτε σημείο του διαφράγματος. Δ.3 Δυσκαμψίες διαφράγματος Κάθε διάφραγμα έχει δύο δυσκαμψίες κατά τις δύο κύριες διευθύνσεις. Δυσκαμψία διαφράγματος Kxx (ή Kyy) προς την κύρια διεύθυνση x (ή y), είναι ο λόγος της σεισμικής δύναμης H προς την αντίστοιχη μετακίνηση δxo (ή δyo) του διαφράγματος, όταν η δύναμη ασκηθεί επί του CTκατά την κύρια διεύθυνση x (ή y), δηλαδή: Kxx = Hxx /δ xxo , Kyy = Hxy /δ xyo ή ισοδύναμα: Kxx = Hyx /δ yxo , Kyy = Hyy /δ yyo Χρησιμοποιώντας τη 2η επίλυση , η εξωτερική δύναμη HX=100 του αρχικού συστήματος X0Y αναλύεται στις δύοισοδύναμες κύριες δυνάμεις Hxx=100·cosa και Hxy=-100·sina (βλέπε §Γ.2) που εξασκούνται στις δύο διευθύνσεις x,y του κύριου συστήματος. Στην προκειμένη περίπτωση έχουν γωνίαa=-6.154º επομένως Hxx=100·0.994=99.4 kN και Hxy=-100· (-0.107)=10.7 kN. Αντίστοιχα οι δύο μετακινήσεις του κέντρου ελαστικής στροφής στο X0Y που έχουν προκύψει από τη 2η επίλυση, είναι δ XXo=2.103, δΧΥο=-0.047 οι οποίες μεταφερόμενες στο κύριο σύστημα δίνουν (§Γ.2): δ xxo = δ XXo · cosa- δ XYo · sina=2.103 ·0.994-(-0.047)·(-0.107)=2.090-0.005=2.085 mm δ xyo =- δ XXo · sina+ δ XYo · cosa=-2.103 ·(-0.107)+(-0.047)·0.994=0.225-0.047=0.178 mm, άρα Kxx=Hxx/ δ xxo =99.4·103N/2.085·10-3m=47.7·106 N/m
Kyy=Hxy/ δ xyo =10.7·103N/0.178·10-3m=60.1·106 N/m
Παρατηρήσεις: - Αν χρησιμοποιηθεί η 3η επίλυση, προκύπτουν
Hyx=100·sina=-10.7 kN και Hyy=100·cosa=99.4 kN δyxo=δYXo·cosa+δYYo·sina=(-0.047)·0.994+1.668·(-0.107)=-0.047-0.178=0.225, δyyo=-δYXo·sina+δYYo·cosa=-(-0.047)·(-0.107)+1.668·(0.994)=-0.005+1.658=1.653 Kxx=Hyx/δyxo=-10.7·103N/(-0.225·10-3m)=47.6·106 N/m Kyy=Hyy/δyyo=99.4·103N/1.653·10-3m=60.1·106 N/m Δηλαδή προκύπτουν οι ίδιες τιμές των δυσκαμψιών όπως αναμενόταν. - Για τον υπολογισμό των δυσκαμψιών Kxx, Kyy θα μπορούσαν να χρησιμοποιηθούν οι εξισώσεις Γ.9.2 και Γ.9.3 της §Γ.9, οπότε:
Kxx=H/(δXXo+δXYo·tana)=100.0/(2.103-0.047·0.107)·106N/m=47.6·106 N/m
Kyy=H/(δYYo-δXYo·tana)=100.0/(1.668+0.047·0.107)·106N/m=60.0·106 N/m - Σε περίπτωση που το κέντρο ελαστικής στροφής συμπίπτει με το κέντρο μάζας, η Kxx θα πρέπει να υπολογίζεται από τη 2η επίλυση και η Kyy από την 3η επίλυση, ώστε σε καμιά περίπτωση να μην προκύψει διαίρεση με το μηδέν.
Δ.4 Δυστρεψία διαφράγματος Δυστρεψία διαφράγματος K θείναι ο λόγος της ροπής MCT που εξασκείται επί του κέντρου ελαστικής στροφής CT, προς τη γωνία στροφής θ z του διαφράγματος.
Η ροπή που εξασκείται επί του CT είναι
MXCT =100.0 · ( YCT - YCM )+100.0 · cY =100 ·(12.685-12.323)+200.0=36.2+200.0=236.2 kNm
K θ = MXCT /θ XZ =236.2 ·103 Nm /4.5613 ·10-5=5178·106 Nm
Παρατήρηση: Η ροπή MXCT των εξωτερικών δυνάμεων οφείλεται σε δύο παράγοντες, στην εξωτερική δύναμη H που δίνει την ροπή MXH=36.2 kNm και στην εξωτερική ροπή MXM=200.0 kNm. Aντίστοιχα, η γωνία στροφής του διαφράγματος θΧΖ οφείλεται στην θXZΗ=(MXH/MXCT)·θXZ=(36.2/236.2)· 4.5613·10-5=0.699·10-5 και θXZM=(MXM/MXCT)·θXZ=(200/236.2)· 4.5613·10-5=3.8622·10-5 Ισχύει επίσης Kθ=MXH/θXZH=MXM/θXZM=5178·106 Nm. Η σταθερή τιμή της ροπής σε όλα τα διαφράγματα και ο αντίστοιχος υπολογισμός της δυστρεψίας αξιοποιείται στον προσδιορισμό του ισοδύναμου συστήματος της §Δ.6. Κατανομή δυστρεψίας διαφράγματος είναι η καμπύλη επί της οποίας, αν τοποθετηθούν, συμμετρικά ως προς το κέντρο ελαστικής στροφής οι ιδεατές κολόνες, των οποίων τα αθροίσματα δυσκαμψιών κατά x καιy είναι ίσα με τις δυσκαμψίες του διαφράγματος κατά x και y αντίστοιχα, δίνουν δυστρεψία ίδια με αυτή του διαφράγματος. 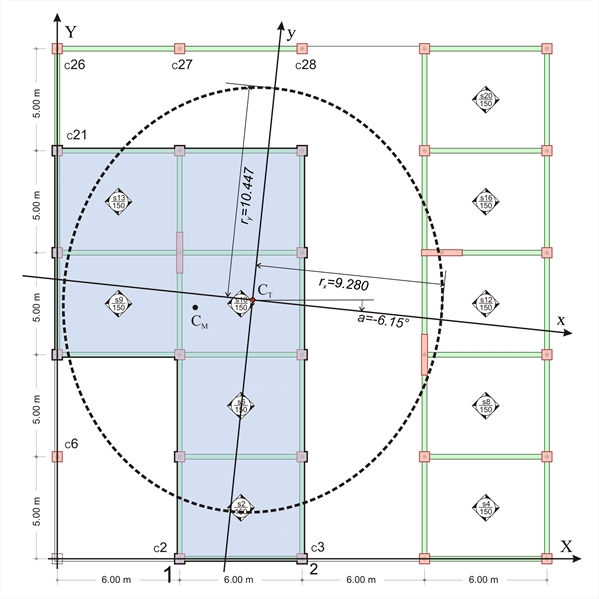 Εικόνα Δ.5
Εικόνα Δ.5 Εικόνα Δ.5
Έλλειψη αδράνειας διαφράγματοςείναι η έλλειψη που έχει κέντρο το CT και ακτίνες rx=√(Kθ/ Kyy), ry=√(Kθ/Kxx). rx =√ K θ / Kyy =√[5178·106Ν m /60.1·106 N / m ]=9.28 m
ry =√ K θ / Kxx =√[5178·106 Nm /47.7·106 N / m ]=10.42 m Δ.6 Ισοδύναμο Σύστημα – Σχετική δυσκαμψία – Σχετική δυστρεψία Στηριζόμενοι στο Παράρτημα Β, §Β.1 και §Β.2 και έχοντας γνώση των προηγούμενων παραγράφων αυτού του παραρτήματος, δημιουργούμε ένα απλό αλλά ισοδύναμο κτίριο. Το ισοδύναμο κτίριο πρέπει να αποτελείται από τον ίδιο αριθμό ορόφων και διαφραγμάτων. Κάθε όροφος πρέπει να έχει κολόνες με συγκεκριμένες διαστάσεις, άρα οι δυσκαμψίες και δυστρεψίες που θα χρησιμοποιηθούν πρέπει να είναι ανά όροφο, επομένως χρησιμοποιούνται οι σχετικές (βλέπε §5.4.3.5 και §5.4.4) Κάθε διάφραγμα αντικαθίσταται από ένα ισοδύναμο διάφραγμα με 4 αμφίπακτες κολόνες συμμετρικές ως προς το κέντρο ελαστικής στροφής του. Το ισοδύναμο διάφραγμα i θεωρούμε ότι θα λειτουργήσει σαν μονώροφο με αμφίπακτες κολόνες. Ορίζω τις 4 σχετικές μετακινήσεις του κέντρουελαστικής στροφής του μονώροφου κατά X, Y, δXXoΖ,i, δXYoΖ, i , δYXoΖ,i, δYYoΖ,i [*] Note Ο δείκτης Z, πριν το ,i δηλώνει ότι η τιμή του συγκεκριμένου μεγέθους είναι η σχετική και όχι η κανονική. και τη γωνία στροφής θXZΜZ,i, να έχουν τις παρακάτω τιμές, συναρτήσει των μετακινήσεων του πραγματικού κτιρίου. Note Ο δείκτης Z, πριν το ,i δηλώνει ότι η τιμή του συγκεκριμένου μεγέθους είναι η σχετική και όχι η κανονική. και τη γωνία στροφής θXZΜZ,i, να έχουν τις παρακάτω τιμές, συναρτήσει των μετακινήσεων του πραγματικού κτιρίου. δ XXo Ζ ,i = δ XXo,i - δ XXo,i-1 , δ XYo Ζ ,i = δ XYo,i - δ XYo,i-1 ,
δ YXo Ζ ,i = δ YXo,i - δ YXo,i-1 [*] NoteΠάντοτε θα είναι dXYoZ,i=dYXoZ,i επειδή ισχύει δXYo,i=δ YXo,i και δXYo,i-1=δYXo,i-1 επομένως το ίδιο θα ισχύει και για τη διαφορά τους. , δ YYo Ζ ,i = δ YYo,i - δ YYo,i-1 , NoteΠάντοτε θα είναι dXYoZ,i=dYXoZ,i επειδή ισχύει δXYo,i=δ YXo,i και δXYo,i-1=δYXo,i-1 επομένως το ίδιο θα ισχύει και για τη διαφορά τους. , δ YYo Ζ ,i = δ YYo,i - δ YYo,i-1 ,
θ XZ Μ Z,i = θ X ΖΜ ,i – θ XZ Μ ,i-1 [*] Note Ο δείκτης M σημαίνει γωνία στροφής του διαφράγματος λόγω ροπής MM=H·c όπως περιγράφεται στην παρατήρηση της §Δ.4. . Note Ο δείκτης M σημαίνει γωνία στροφής του διαφράγματος λόγω ροπής MM=H·c όπως περιγράφεται στην παρατήρηση της §Δ.4. . Επομένως, το ισοδύναμο διάφραγμα θα έχει γωνία κυρίου συστήματος az,i=2δXYoΖ,i/( δ XXoΖ,i- δYYoΖ,i), δυστρεψία KθZ,i=H·cY/ θXZΜZ,i , δυσκαμψίες KxxZ,i= H/(δXXoZ,i+δXYoZ,i·tanaZ,i) και KyyΖ,ι=H/(δYYoZ,i-δ XYoZ,i·tanaZ,i) (εξισώσεις Γ.9.2 και Γ.9.3 της §Γ.9). Επίσης rxZ,i=√KθZ,i/KyyZ,i, ryZ,i=√KθZ,i/KxxZ,i
Τοποθετούμε τα ισοδύναμα διαφράγματα μετατοπίζοντας το κέντρο ελαστικής στροφής τους στο σημείο 0.0, 0.0. Έτσι δημιουργείται το ισοδύναμο κτίριο που το τυχόν διάφραγμα του i θα δίνει τα παρακάτω μεγέθη: δ XXo_equal,i = Σ ( δ XXo Ζ ,k ) όπου k=i έως 1 → δXXo_equal,i=Σ(δXXo,i-δXXo,i-1)= (δXXo,i-δXXo,i-1)+ (δXXo,i-1-δXXo,i-2)+…+ (δXXo,1-0.0)=δXXo,i → δXXo_equal,i= δXXo,i Με την ίδια λογική δXYo_equal,i=δXYo,i , δYYo_equal,i=δYYo,i και θXZ_equal,i = θXZΜ,i Επομένως και όλα τα διαφραγματικά του μεγέθη Kxx_equal,i ,Kyy_equal,i , Kθ_equal, i θα είναι ίδια με αυτά του πραγματικού κτιρίου. Ως αναλυτικά παραδείγματα εφαρμογής χρησιμοποιούνται τα 2 της επόμενης παραγράφου. Η αξιολόγηση σε σεισμό, του φορέα του πραγματικού κτιρίου, μπορεί να γίνει εύκολα, άμεσα και εποπτικά χρησιμοποιώντας το ισοδύναμο κτίριο. - Στα ισόγεια διαφράγματα, η έλλειψη δυσκαμψίας και η έλλειψη δυσκαμψίας των αντίστοιχων ισοδύναμων διαφραγμάτων, συμπίπτουν.
- Ισχύει: 1/Kθ_equal,i=Σ(1/KθΖ,j), j από 1 έως και i
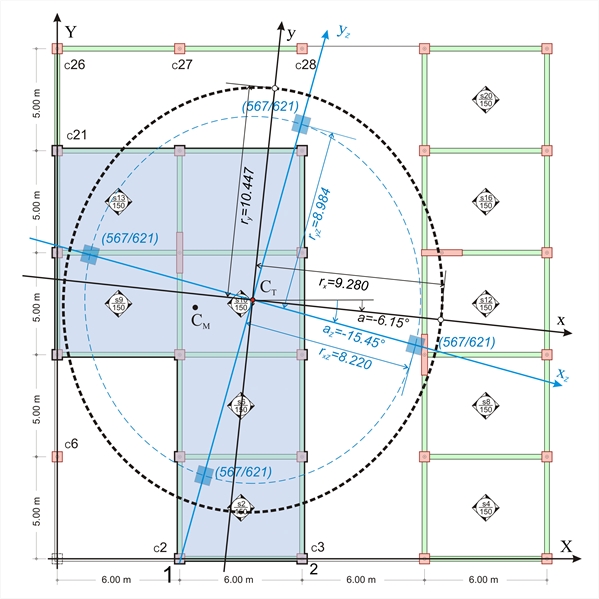 Εικόνα Δ.6: Το ισοδύναμο διάφραγμα του αριστερού διαφράγματος του 4ου ορόφου (περίπτωση n=4 ισοδύναμων κολονών διατομής 567/621)
Εικόνα Δ.6: Το ισοδύναμο διάφραγμα του αριστερού διαφράγματος του 4ου ορόφου (περίπτωση n=4 ισοδύναμων κολονών διατομής 567/621) Εικόνα Δ.6: Το ισοδύναμο διάφραγμα του αριστερού διαφράγματος του 4ου ορόφου (περίπτωση n=4 ισοδύναμων κολονών διατομής 567/621)
(περίπτωση n=4 ισοδύναμων κολονών διατομής 567/621) |