Τέμνουσες δυνάμεις και αντιδράσεις στήριξης Όταν μία πλάκα στηρίζεται και στις τέσσερις παρυφές και ο λόγος του μεγαλύτερου προς το μικρότερο θεωρητικό άνοιγμα είναι ≤2.00, θεωρείται τετραέρειστη. Οι τετραέρειστες πλάκες υπό ομοιόμορφο φορτίο επιλύονται στατικά με πίνακες, από τους οποίους προκύπτουν οι θεμελιώδεις ροπές στηρίξεων, οι ροπές ανοιγμάτων και οι τέμνουσες δυνάμεις. Στους πίνακες αυτούς, ανάλογα με τον τρόπο στήριξης, κάθε πλάκα χαρακτηρίζεται από έναν αριθμό από 1 έως 6, όπως απεικονίζεται στο επόμενο σχήμα: Το διάφραγμα ενός ορόφου περιλαμβάνει κατά κανόνα πολλές πλάκες σε επαφή μεταξύ τους και η κάθε πλάκα επηρεάζει τις υπόλοιπες. Ο ακριβής υπολογισμός των επιρροών αυτών πραγματοποιείται μόνο με τη χρησιμοποίηση επιφανειακών πεπερασμένων στοιχείων. Στις συνήθεις περιπτώσεις, οι γειτονικές πλάκες δεν επηρεάζουν σημαντικά τις τέμνουσες δυνάμεις και τις αντιδράσεις μίας τετραέρειστης πλάκας. Για το λόγο αυτό, και για να είναι εφικτός ο υπολογισμός με απλά υπολογιστικά μέσα, εξετάζουμε κάθε πλάκα χωριστά. Η κατανομή του φορτίου είναι τριγωνική ή τραπεζοειδής. Τα ύψη των τριγώνων/τραπεζίων ορίζουν τις μέγιστες τιμές του φορτίου που μεταβιβάζεται στα αντίστοιχα σημεία της περιμετρικής στήριξης. Τα μέγιστα αυτά φορτία είναι οι μέγιστες τέμνουσες δυνάμεις Vi,j της πλάκας, ενώ τα ισοδύναμα φορτία pi,j είναι οι ισοδύναμες ομοιομορφισμένες αντιδράσεις. Η κατανομή των αντιδράσεων μπορεί να υπολογισθεί με τον ακόλουθο απλοποιημένο κανόνα: 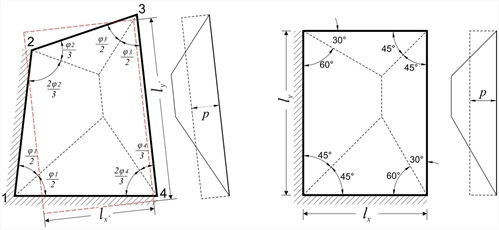 Εικόνα 4.6.1.1-1
Εικόνα 4.6.1.1-1 Εικόνα 4.6.1.1-1 - Στην τομή δύο όμοιων παρυφών (πακτωμένων ή ελεύθερα στρεπτών) το φορτίο διανέμεται με γωνία μερισμού φ/2 (45ο για ορθογωνική πλάκα).
- Στην τομή δύο ανόμοιων παρυφών (μια πάκτωση και μια ελεύθερα στρεπτή), το φορτίο διανέμεται με γωνία μερισμού 2φ/3 προς την πλευρά της πακτωμένης παρυφής (60º για την ορθογωνική) και φ/3 προς την πλευρά της ελεύθερα στρεπτής (30º για την ορθογωνική).
- Στο παράδειγμα του προηγούμενου σχήματος, η ισοδύναμη ορθογωνική πλάκα υποδει-κνύεται με διακεκομμένη κόκκινη γραμμή. Οι διαστάσεις της s lx', l y' έχουν προκύψει με την παραδοχή ίδιου εμβαδού και ίδιων ροπών αδρανείας.
- Ο παραπάνω κανόνας για τη διανομή του φορτίου ισχύει και για πλάκες με περισσότερες από τέσσερις πλευρές.
- Η κατανομή του φορτίου που υιοθετούμε προσεγγίζει σημαντικά την αντίστοιχη πραγματική, που προκύπτει με τη θεωρία της ελαστικότητας. Στην πράξη, η τραπεζοειδής φόρτιση ανάγεται σε ισοδύναμη ορθογωνική, όπως διακρίνεται στα προηγούμενα σχήματα.
- Όσες στηρίξεις δεν έχουν ληφθεί υπόψη στον υπολογισμό μιας πλάκας, πρέπει να συμ-μετέχουν στη διανομή των φορτίων.
- Η ίδια λογική είναι δυνατόν να εφαρμοσθεί στις τριέρειστες και διέρειστες πλάκες.
Οι τιμές των συντελεστών των τεμνουσών δυνάμεων Vi,j και των ισοδύναμων ομοιόμορφων αντιδράσεων pi,j δίνονται στους έξι πίνακες b5.1 έως b5.6 που παρατίθενται στο τέλος του βιβλίου. 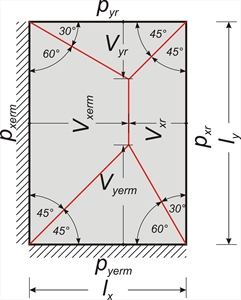 Εικόνα 4.6.1.1-2
Εικόνα 4.6.1.1-2 Εικόνα 4.6.1.1-2 Σε καθεμία από τις έξι περιπτώσεις στηρίξεων σχηματίζονται δύο τρίγωνα και δύο τραπέζια κατά τις διευθύνσεις x, y ή αντίστροφα (ανάλογα με το λόγο των πλευρών). Στη συνέχεια, εξετάζεται η γενική περίπτωση πλάκας για τους 2 λόγους πλευρών για τους οποίους ισχύει S≥0 (όπως φαίνεται στα δύο επόμενα σχήματα). Με βάση τις εξισώσεις που προκύπτουν έχουν καταρτισθεί οι πίνακες b5.
Γενικός απλοποιημένος υπολογισμός Τεμνουσών και Αντιδράσεων 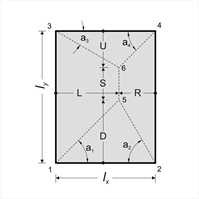 Εικόνα 4.6.1.1-3
Εικόνα 4.6.1.1-3 Εικόνα 4.6.1.1-3
VL=L x p=ρL x p x lx, VR=R x p=ρR x p x lx, VD=D x p=ρD x p x lx, VU=U x p=ρU x p x lx pL=(A1,3,6,5 x p)/ly=υL x p x lx pR=(A2,4,6,5 x p)/ly=υR x p x lx, pD=(A1,2,5 x p)/lx=υD x p x lx pU=(A3,4,6 x p)/lx=υU x p x lx | 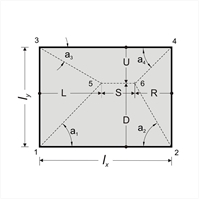 Εικόνα 4.6.1.1-4
Εικόνα 4.6.1.1-4 Εικόνα 4.6.1.1-4
VL=L x p=ρL x p x lx, VR=R x p=ρR x p x lx, VD=D x p=ρD x p x lx, VU=U x p=ρU x p x lx pL=(A1,3,5 x p)/ly=υL x p x lx pR=(A2,4,6 x p)/ly=υR x p x lx, pD=(A1,2,6,5 x p)/lx=υD x p x lx pU=(A3,4,6,5) x p/lx=υU x p x lx | D=[1/(cota1+cota2)] x lx=ρD x lx , where ρD=1/(cota1+cota2) U=[1//(cota3+cota4)] x lx=ρU x lx , where ρU=1/(cota3+cota4) L=[cota1/(cota1+cota2)] x lx=ρL x lx , όπου ρL=cota1/(cota1+cota2) R=[cota2/(cota1+cota2)] x lx=ρR x lx , όπου ρR=cota2/(cota1+cota2) pL=A1,3,6,5/ly=0.50 x (ly+S) x L/(ε x lx)=0.50 x (2ε-ρD-ρU) x ρL x lx x lx/ (ε x lx)= =υL x p x lx , where υL=[0.50x (2ε-ρD-ρU)xρL]/ε pR=A2,4,6,5/ly=0.50 x (ly+S) x R/(ε x lx)=0.50 x (2ε-ρD-ρU) x ρR x lx x lx/(ε x lx)= =υR x p x lx , όπου υR=[0.50x (2ε-ρD-ρU)xρR]/ε pD=(A1,2,5 x p)/lx=0.50 x lx x D/lx=0.50 x ρD x lx , όπουυD=0.50 xρD pU=(A3,4,6 x p)/lx=0.50 x lx x U/lx=0.50 x ρU x lx , where<υU=0.50xρU Επαλήθευση: (α) S≥0, (b) L+R=lx, (c) υL+υR+(υD+υU)/ε=1.0 Παράδειγμα: τύπος πλάκας 4, lx=4.0 m, ly=6.0 m, p=15.0 kN/m2 ε=ly/lx=6.0/4.0=1.5. Για πλάκα τύπου 4 a1=45°, a2=60°, a3=30°, a4=45°, οπότε ρyerm=ρD=0.634, ρyr=ρU=0.366, ρxerm=ρL=0.634, ρxr=ρR=0.366 S=(1.5-0.634-0.366) x lx=0.50 x lx υxerm=υL=[0.50 x(2x1.5-0.634-0.366) x0.634]/1.5=0.423 υxr=υR=[0.50 x(2x1.5-0.634-0.366) x0.366]/1.5=0.244 υyerm=υD=0.50 x ρD=0.50 x0.634=0.317 υyr=υU=0.50 x ρU=0.50 x0.366=0.183 Vxerm=ρxerm x p x lx=0.634 x15.0x4.0=38.04 kN/m Vxr= ρxr x p x lx=0.366 x15.0x4.0=21.96 kN/m Vyerm= ρyerm x p x lx=0.634 x15.0x4.0=38.04 kN/m Vyr= ρyr x p x lx=0.366 x15.0x4.0=21.96 kN/m pxerm=υxerm x p x lx=0.423 x15.0x4.0=25.38 kN/m pxr= υxr x p x lx=0.244 x15.0x4.0=14.64 kN/m pyerm= υyerm x p x lx=0.317 x15.0x4.0=19.02 kN/m pyr= υyr x p x lx=0.183 x15.0x4.0=10.98 kN/m | L=[1/(tana1+tana3)] x ly=ρL x lx, where ρL=ε/(tana1+tana3) R=[1/(tana2+tana4)] x ly=ρR x lx, where ρR=ε/(tana2+tana4) D=[tana1/(tana1+tana3)] x ly=ρD x lx, όπου ρD=(εxtana1)/(tana1+tana3) U=[tana2/(tana1+tana3)] x ly=ρU x lx, όπου ρU=(εxtana3)/(tana1+tana3) pL=(A1,3,5 x p)/ly=0.50 x ly x L/ly=0.50 x ρL x lx, όπου υL=0.50 xρL pR=(A2,4,6 x p)/lx=0.50 x ly x R/ly=0.50 x ρU x lx, where υR=0.50x ρR pD=A1,2,6,5/lx=0.50 x (lx+S) x D/lx=0.50 x (2-ρL-ρR) x ρD x lx x lx/lx=υD x p x lx, where υD=0.50x(2-ρL-ρR)xρD pU=A3,4,6,5/lx=0.50 x (lx+S) x U/lx=0.50 x (2-ρL-ρR) x ρU x lx x lx/lx=υU x p x lx, όπου υU=0.50x(2-ρL-ρR)xρU Επαλήθευση: (a) S≥0, (b) D+U=εxlx, (c) υL+υR+(υD+υU)/ε=1.0 Παράδειγμα: τύπος πλάκας 4, lx=6.0 m, ly=4.0 m, p=15.0 kN/m2 ε=ly/lx=4.0/6.0=2/3. Για τύπο πλάκας 4 a1=45°, a2=60°, a3=30°, a4=45°, οπότε ρxerm=ρL=0.423, ρxr=ρR=0.244, ρyerm=ρD=0.423, ρyr=ρU=0.244, S=(1-0.423-0.244) x lx=0.333 x lx υxerm=υL=0.50 x ρL=0.50 x0.423=0.212 υxr=υR=0.50 x ρR=0.50 x0.244=0.122 υyerm=υD=0.50 x(2-0.423-0.244)x0.423=0.282 υyr=υU=0.50 x(2-0.423-0.244)x0.244=0.163 Vxerm=ρxerm x p x lx=0.423 x15.0x6.0=38.07 kN/m Vxr=ρxr x p x lx=0.244 x15.0x6.0=21.96 kN/m Vyerm= ρyerm x p x lx=0.423 x15.0x6.0=38.07 kN/m Vyr= ρyr x p x lx=0.244 x15.0x6.0=21.96 kN/m pxerm=υxerm x p x lx=0.212 x15.0x6.0=19.08 kN/m pxr= υxr x p x lx=0.122 x15.0x6.0=10.98 pyerm=υyerm x p x lx=0.282 x15.0x6.0=25.38 kN/m pyr= υyr x p x lx=0.163 x15.0x6.0=14.67 kN/m |
Μέθοδος ελαστικότητας κατά Czerny 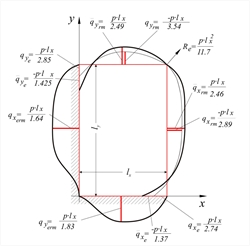 Εικόνα 4.6.1.2-1
Εικόνα 4.6.1.2-1 Εικόνα 4.6.1.2-1 Σύμφωνα με τη θεωρία της ελαστικότητας, η κατανομή των τεμνουσών δυνάμεων κατά μήκος των τεσσάρων πλευρών της πλάκαςπροκύπτει από τις τέμνουσες δυνάμεις στην περίμετρο της πλάκας, οι οποίες περιγράφονται με εξισώσεις. Οι δυσμενέστερες τέμνουσες κατά μήκος των πλευρών μίας πλάκας (όπως και οι δυσμενέστερες ροπές) παρέχονται από τους πίνακες του βιβλίου των Πινάκων με τίτλο “Εφαρμογές Οπλισμένου Σκυροδέματος” (σελίδες 46 έως 51 για τετραέρειστες, 52 έως 59 για τις τριέρειστες και τις διέρειστες) της σειράς των βιβλίων του Απόστολου Κωνσταντινίδη του 1994. 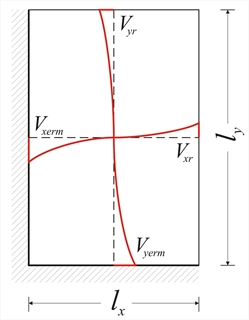 Εικόνα 4.6.1.2-2
Εικόνα 4.6.1.2-2 Εικόνα 4.6.1.2-2 Ανάλογα με το λόγο ε = lx / ly (όπου lx η μικρότερη διάσταση) και τον τύπο της στήριξης, οι τέμνουσες δυνάμεις στις παρυφές ισούνται με:
- Η απλοποιημένη μέθοδος δίνει δυσμενέστερες τέμνουσες δυνάμεις από τους παραπάνω πίνακες.
- Τόσο οι εξισώσεις ελαστικότητας, όσο και οι αντίστοιχοι πίνακες, αναφέρονται σε μία μόνο ορθογωνική πλάκα, ή σε συμμετρικούς συνδυασμούς ορθογωνικών πλακών. Η γενική λύση διαφόρων σχημάτων και τυχούσας διάταξης πλακών επιτυγχάνεται με ακρίβεια μόνο με πεπερασμένα στοιχεία.
>Δύο από τις μεθόδους υπολογισμού είναι: η μέθοδος Marcus και η μέθοδος Czerny.
|