Δυσκαμψία υποστυλώματος πλαισίου
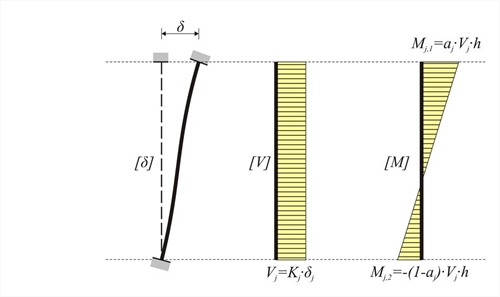Εικόνα 5.1.5: Δυσκαμψία υποστυλώματος πλαισίου κατά τη διεύθυνση j (j=x, y) Εικόνα 5.1.5: Δυσκαμψία υποστυλώματος πλαισίου κατά τη διεύθυνση j (j=x, y)
Στη γενική περίπτωση υποστυλώματος πλαισίου, η δυσκαμψία K προς μία διεύθυνση j ισούται με:
Ο συντελεστής kj ονομάζεται συντελεστής δυσκαμψίας και γενικά λαμβάνει τιμές μεταξύ 0 and 12.Προς την ίδια διεύθυνση υπάρχει και ο συντελεστής aj ο οποίος καλείται συντελεστής κατανομής της ροπής και οι τιμές του κυμαίνονται συνήθως μεταξύ 0.0 and 1.0.
Ισχύει πάντα Mj,1 - Mj,2 = Vj· h
Ο συντελεστής μείωσης της δυσκαμψίας λόγω τεμνουσών δυνάμεων ισούται με:
Η αποτίμηση των δυσκαμψιών απαιτείται για την κατανόηση του Διαφραγματικού Ορόφου που ακολουθεί στην §5.4.
Τα πλαίσια μπορεί να αποτελούνται μόνο από υποστυλώματα ή από υποστυλώματα και τοιχία, τα πρώτα τα ονομάζουμε “ πλαισιακά συστήματα” και τα δεύτερα “μικτά συστήματα”. Αυτά τα δύο είδη πλαισίων εξετάζονται στη συνέχεια.
5.1.5.1 Μονώροφα πλαισιακά στατικά συστήματα
Στη μελέτη του συνοδευτικού λογισμικού, τα τρία υποστυλώματα έχουν διατομή 400/400 και ύψος 3.0 m, ενώ τα ζυγώματα έχουν ως διατομή πλακοδοκό 300/500/1300/150 και άνοιγμα 6.0 m. Η σεισμική οριζόντια δύναμη ισούται με 50 kN.
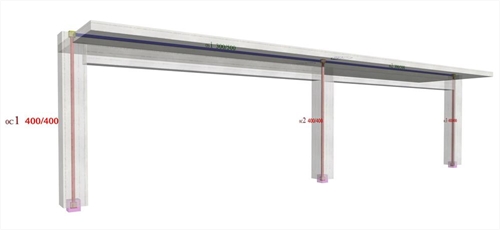Εικόνα 5.1.5.1-1: Το πλαίσιο του παραδείγματος χωρίς στερεά σώματα με το 100% των ελαστικών δυσκαμψιιών, μελέτη <B_5151a> Εικόνα 5.1.5.1-1: Το πλαίσιο του παραδείγματος χωρίς στερεά σώματα με το 100% των ελαστικών δυσκαμψιιών, μελέτη <B_5151a>
Οι τιμές των παραμέτρων για τη συγκεκριμένη προσομοίωση είναι ίδιες με τις αντίστοιχες πα-ραμέτρους του παραδείγματος B_513 της §5.1.3 μόνο που η δύναμη X έχει δοθεί = 50.
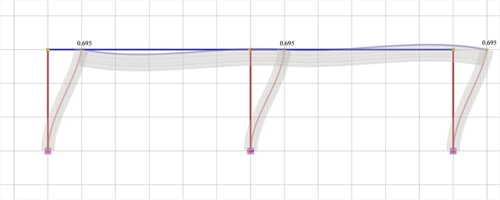Εικόνα 5.1.5.1-2: Ελαστική γραμμή, δ=0.695 mm Εικόνα 5.1.5.1-2: Ελαστική γραμμή, δ=0.695 mm |
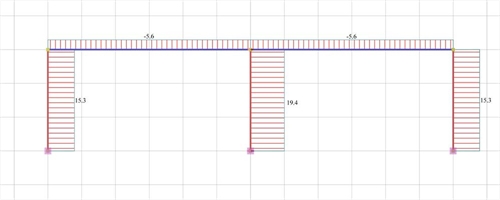Εικόνα 5.1.5.1-3: Διάγραμμα τεμνουσών δυνάμεων Εικόνα 5.1.5.1-3: Διάγραμμα τεμνουσών δυνάμεων |
Εικόνα 5.1.5.1-4: Διάγραμμα ροπών κάμψης Εικόνα 5.1.5.1-4: Διάγραμμα ροπών κάμψης |
Αποτελέσματα της μελέτης με πλήρεις δυσκαμψίες στις δοκούς και κολόνες (όπως αποδίδεται γραφικά από το συνοδευτικό λογισμικό)
Η πραγματική δυσκαμψία των C1, C3 ισούται με:
K1=K3=V1/ δ =15.3·103N/0.000695m=22.01·106 kN/m
έναντι του 31.10·106 N/m της αμφίπακτης.
Επομένως ο συντελεστής δυσκαμψίας προκύπτει ίσος με:
ενώ ο συντελεστής κατανομής της ροπής a, δηλαδή το ποσοστό της ροπής V · h που εξασκείται στην κορυφή της κολόνας ίσος με:
Η πραγματική δυσκαμψία του υποστυλώματος C2 ισούται με:
K2=V2/ δ =19.4·103N/0.0006955m=27.91·106 kN/m
έναντι του 31.10·106 N/m της αμφίπακτης.Οι αντίστοιχοι συντελεστές προκύπτουν ίσοι με:
Το μεσαίο υποστύλωμα, παρόλο που έχει την ίδια διατομή με τα ακραία, εμφανίζει μεγαλύτερη δυσκαμψία καθώς σε αυτό συντρέχουν δύο δοκοί που αντιστέκονται στην κάμψη του.
H μελέτη είναι ίδια με τη μελέτη με τη διαφορά ότι έχει επιπλέον θεμε-λίωση στη στάθμη -0.80 m με πεδιλοδοκούς διατομής 300/800/1500/400.
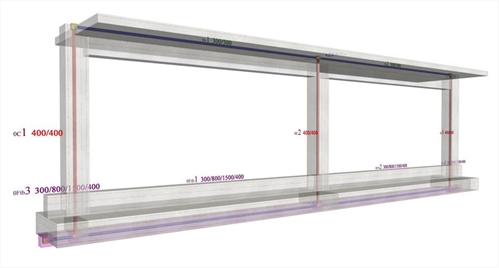Εικόνα 5.1.5.1-5: Το πλαίσιο της μελέτης <B_5151b> με τις πλήρεις δυσκαμψίες Εικόνα 5.1.5.1-5: Το πλαίσιο της μελέτης <B_5151b> με τις πλήρεις δυσκαμψίες
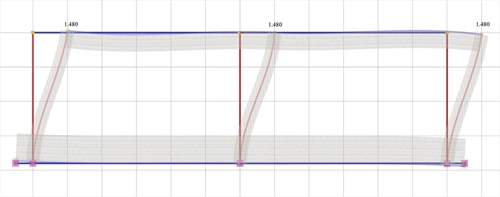Εικόνα 5.1.5.1-6: Ελαστική γραμμή, δ=1.480 mm Εικόνα 5.1.5.1-6: Ελαστική γραμμή, δ=1.480 mm |
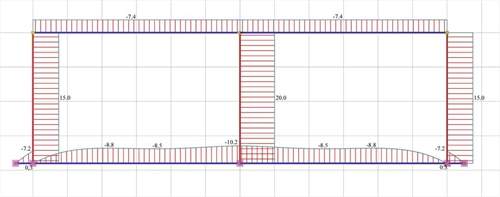Εικόνα 5.1.5.1-7: Διάγραμμα τεμνουσών δυνάμεων Εικόνα 5.1.5.1-7: Διάγραμμα τεμνουσών δυνάμεων |
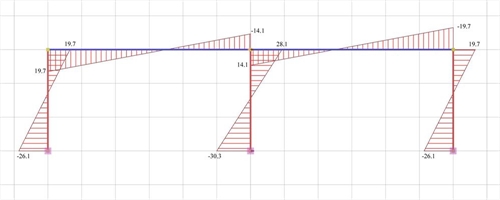
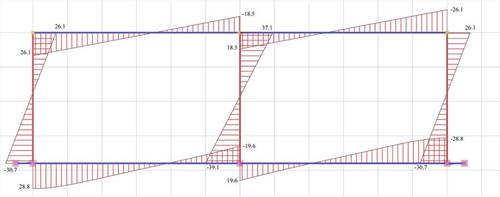Εικόνα 5.1.5.1-8: Διάγραμμα ροπών κάμψης Εικόνα 5.1.5.1-8: Διάγραμμα ροπών κάμψης |
Αποτελέσματα της μελέτης με πραγματικές δυσκαμψίες στις δοκούς και κολόνες (όπως αποδίδεται γραφικά από το συνοδευτικό λογισμικό)
Η πραγματική δυσκαμψία των C1, C3 ισούται με:
K1=K3=V1/ δ =15.0·103N/0.001480m=10.14·106 kN/m
έναντι του K=12·EI/h3=12·(32.8·109·Ν/m)2·(21.33·10-4m4)/(3.803·m3)=15.30·106 N/m της αμφίπακτης, η οποία στη συγκεκριμένη περίπτωση έχει ύψος 3.80 m.
Ο συντελεστής δυσκαμψίας προκύπτει ίσος με:
ενώ ο συντελεστής κατανομής της ροπής a,δηλαδή το ποσοστό της ροπής V·h που εξασκείται στην κορυφή της κολόνας ίσος με:
Η πραγματική δυσκαμψία του υποστυλώματος C2 ισούται με:
K2=V2/ δ =20.0·103N/0.001480m=13.51·106 kN/m
έναντι του 15.30·106 N/m της αμφίπακτης. Οι αντίστοιχοι συντελεστές προκύπτουν ίσοι με:
k2=12·13.51/15.30=10.6 and a=178.0/(178.0+187.8)=0.49
Οι κόμβοι της θεμελίωσης βρίσκονται κοντά στο έδαφος, διότι υπάρχει και το “μέλος” του εδάφους εκτός από τα μέλη των υποστυλωμάτων και των δοκών θεμελίωσης, στην οποία θα πρέ-πει να δώσουμε ιδιαίτερη βαρύτητα. Οι διαφορές στις δυσκαμψίες των κολονών οφείλονται κυρίως στο διαφορετικό μικτό ύψος. Το μικτό ύψος ενός υποστυλώματος ισούται με το ελεύθερο ύψος του ορόφου της θεμελίωσης αυξημένο κατά το ύψος της εκσκαφής. Το ύψος της εκσκαφής είναι συνήθως ίσο με το ύψος των θεμελίων.
- Η επίλυση αυτή έχει πραγματοποιηθεί για ένα μέσο τύπο εδάφους. Στην περίπτωση πιο ελαστικού εδάφους, η μείωση των δυσκαμψιών είναι μεγαλύτερη..
- Αν στη θεμελίωση τοποθετήσουμε μεμονωμένα πέδιλα χωρίς συνδετήριες δοκούς, τότε οι δυσκαμψίες προκύπτουν πολύ μικρότερες και η μετατόπιση των ζυγωμάτων πολύ μεγαλύτερη.
- Αν πριν τη θεμελίωση μεσολαβεί υπόγειο, οι δυσκαμψίες προκύπτουν ισχυρότερες και η μετατόπιση μικρότερη.
5.1.5.2 Μικτά μονώροφα στατικά συστήματα
Στη μελέτη του συνοδευτικού λογισμικού, οι 2 ακραίες κολόνες είναι υποστυλώματα διατομής 400/400 με ύψος 3.0 m και η μεσαία είναι τοιχίο διατομής 2000/300 με ύψος 3.0 m. Το άνοιγμα των ζυγωμάτων είναι 6.0 mενώ η πλακοδοκός έχει διατομή 300/500/1300/150. Η σεισμική οριζόντια δύναμη λαμβάνεται ίση με 50 kN.
Εικόνα 5.1.5.2-1: Μονώροφο μικτό πλαίσιο με 2 υποστυλώματα και ένα τοιχίο στο project <B_5152a> Εικόνα 5.1.5.2-1: Μονώροφο μικτό πλαίσιο με 2 υποστυλώματα και ένα τοιχίο στο project <B_5152a>
Οι τιμές των παραμέτρων της προσομοίωσης λαμβάνονται ίδιες με τις παραμέτρους των πλαισιακών συστημάτων της προηγούμενης παραγράφου.
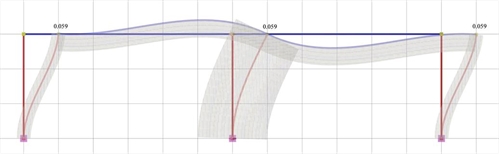Εικόνα 5.1.5.2-2: Ελαστική γραμμή, δ=0.059 mm Εικόνα 5.1.5.2-2: Ελαστική γραμμή, δ=0.059 mm |
Εικόνα 5.1.5.2-3: Διάγραμμα τεμνουσών δυνάμεων Εικόνα 5.1.5.2-3: Διάγραμμα τεμνουσών δυνάμεων |
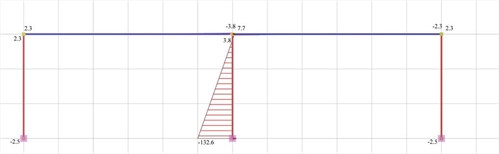Εικόνα 5.1.5.2-4: Διάγραμμα ροπών κάμψης Εικόνα 5.1.5.2-4: Διάγραμμα ροπών κάμψης |
Αποτελέσματα της μελέτης με πραγματικές δυσκαμψίες στις δοκούς και κολόνες (όπως αποδίδεται γραφικά από το συνοδευτικό λογισμικό)
Η πραγματική δυσκαμψία των υποστυλωμάτων C1, C3 ισούται με:
K1=K3=V1/ δ =1.6·103N/0.0000589m=27.16·106 kN/m
έναντι του 31.10·106 N/m της αμφίπακτης.
Ο συντελεστής δυσκαμψίας προκύπτει ίσος με:
k1=k3=12·27.16/31.10=10.5
ενώ ο συντελεστής κατανομής της ροπής a, δηλαδή το ποσοστό της ροπής V·h που εξασκείται στην κορυφή της κολόνας, ίσος με:
Η πραγματική δυσκαμψία του υποστυλώματος C2 ισούται με:
K2=V2/ δ =46.8·103N/0.0000589m=794.6·106 kN/m
έναντι K=12·EI/h3=12·(32.8·109·Ν/m2)·(0.3·2.03/12m4)/(3.03·m3)=2915.56·106 N/ m της αμφίπακτης. Οι αντίστοιχοι συντελεστές προκύπτουν ίσοι με:
k2=12·794.6/2915.56=3.3 και a=7.7/(7.7+132.6)=0.05
Συμπεραίνουμε, λοιπόν, ότι το τοιχίο συμπεριφέρεται σχεδόν σαν μονόπακτο (με k=3.0 καιa=0.0), ), ενώ τα υποστυλώματα σχεδόν σαν αμφίπακτα (με k=12 και a=0.50). Αν ληφθεί υπόψη η τέμνουσα, η μετατόπιση του ζυγώματος ισούται με δ=0.075 mm δηλαδή σημαντικά μεγαλύτερη, ενώ αν ληφθούν υπόψη και τα στερεά σώματα, η μετατόπιση του ζυγώματος προκύπτει ίση με δ=0.070 mm δηλαδή μειώνεται.
H μελέτη είναι ίδια με την με μοναδική διαφορά το γεγονός ότι έχει επι-πλέον θεμελίωση με πλακοδοκούς διατομής 300/800/1500/400 στη στάθμη -0.80 m..
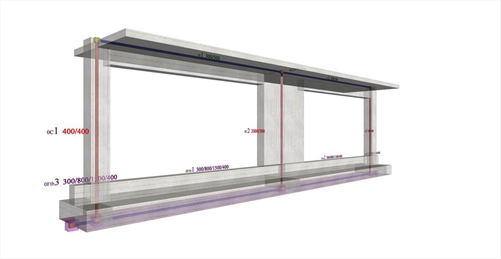Εικόνα 5.1.5.2-5: Το πλαίσιο του παραδείγματος με την πραγματική δυσκαμψία στο project <B_5152b> Εικόνα 5.1.5.2-5: Το πλαίσιο του παραδείγματος με την πραγματική δυσκαμψία στο project <B_5152b>
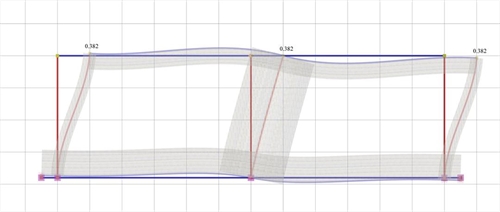Εικόνα 5.1.5.2-6: Ελαστική γραμμή, δ=0.382 mm Εικόνα 5.1.5.2-6: Ελαστική γραμμή, δ=0.382 mm |
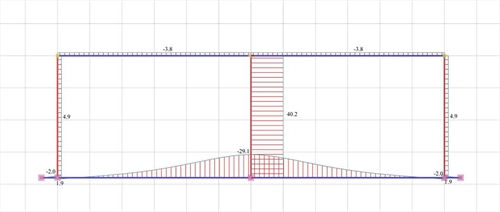Εικόνα 5.1.5.2-7: Διάγραμμα τεμνουσών δυνάμεων Εικόνα 5.1.5.2-7: Διάγραμμα τεμνουσών δυνάμεων |
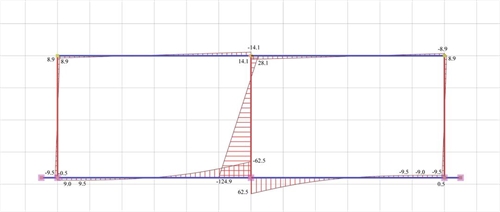Εικόνα 5.1.5.2-8: Διάγραμμα ροπών κάμψης Εικόνα 5.1.5.2-8: Διάγραμμα ροπών κάμψης |
Αποτελέσματα της μελέτης με πραγματικές δυσκαμψίες στις δοκούς και κολόνες (όπως αποδίδεται γραφικά από το συνοδευτικό λογισμικό)
Η πραγματική δυσκαμψία των υποστυλωμάτων C1, C3 ισούται με:
K1=K3=V1/ δ =4.9·103N/0.000382m=12.83·106 kN/m
έναντι του K=12·EI/h3=12·(32.8·109·Ν/m2)·(21.33· 10-4m4)/(3.83·m3)=15.30·106 N/m της αμφίπακτης, η οποία στη συγκεκριμένη περίπτωση έχει ύψος 3.80 m.
Επομένως ο συντελεστής δυσκαμψίας προκύπτει ίσος με:
k1=k3=12·12.83/15.30=10.1
ενώ ο συντελεστής κατανομής της ροπής a ίσος με:
Η πραγματική δυσκαμψία του υποστυλώματος C2 ισούται με:
K2=V2/ δ =40.2·103N/0.000382m=105.24·106 kN/m
έναντι του K=12·EI/h3=12·(32.8 ·109·Ν/m2)·(0.3·2.03 /12) m4/(3.83·m3)=1434.61·10 6 N/m της αμφίπακτης.
Οι αντίστοιχοι συντελεστές προκύπτουν ίσοι με:
k2=12·105.24/1434.61=0.88 and a=28.1/(28.1+124.9)=0.18
Παρατηρούμε ότι η θεμελίωση επηρεάζει σε μεγάλο βαθμό τη δυσκαμψία του τοιχίου, καθώς επίσης και ότι η μετατόπιση των ζυγωμάτων είναι πολύ μεγαλύτερη. Αν ληφθεί υπόψη η τέμνουσα, η μετατόπιση του ζυγώματος προκύπτει ίση με δ=0.399 mm, δηλαδή ελάχιστα μεγαλύτερη. Αν ληφθούν υπόψη δε και τα στερεά σώματα, η συγκεκριμένη μετατόπιση μειώνεται σχεδόν στο μισό λαμβάνοντας την τιμή δ=0.176 mm.
- Η επίλυση αυτή έχει πραγματοποιηθεί για ένα μέσο τύπο εδάφους. Η μείωση των δυ-σκαμψιών είναι μεγαλύτερη για πιο ελαστικό έδαφος.
- Αν μεσολαβεί υπόγειο πριν από τη θεμελίωση, τα υποστυλώματα εμφανίζονται ισχυρότερα με μεγαλύτερες τιμές δυσκαμψίας.