Για τις οριζόντιες συνιστώσες της σεισμικής δράσης το φάσμα σχεδιασμού, S_d(T), ορίζεται από τις ακόλουθες εκφράσεις:

0 ≤ T < T_B:

T_B ≤ T < T_C:

T_C ≤ T < T_D:

T_D ≤ T:

Όπου β=0.20 η συνιστώμενη τιμή του EC8.

Παράδειγμα 1^ο : για κατηγορία σπουδαιότητας II → γ_I = 1.0, τύπο εδάφους B → S = 1.2, σεισμική ζώνη μεa_gR = 0.24 και q = 4.5, για τιμές του Τ 0.1, 0.25, 1.0 και 3.0, λαμβάνουμε αντίστοιχες τιμές του S_d are 0.171g, 0.16g, 0.08g και0.048g.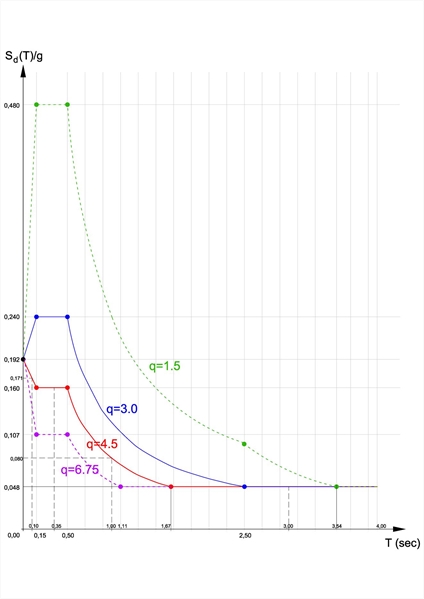

Εικόνα 6.1.6: Φάσμα σχεδιασμού οριζόντιων δυνάμεων (α) για q=4.5, (β) για q=3.0 και (γ) για q=1.5. Ζώνη σεισμικότητας με a_gR=0.24, TD=2.5, Τύπος εδάφους B, κατηγορία σπουδαιότητας ΙΙ

Εικόνα 6.1.6: Φάσμα σχεδιασμού οριζόντιων δυνάμεων (α) για q=4.5, (β) για q=3.0 και (γ) για q=1.5. Ζώνη σεισμικότητας με a_gR=0.24, TD=2.5, Τύπος εδάφους B, κατηγορία σπουδαιότητας ΙΙ

Για a_gR = 0.24, S = 1.2, γ _I = 1.0 έχουμε γ _I · a_gR · S = 1.0 ·0.24·1,2 = 0.288.

και για 4 διαφορετικά q έχουμε τις παρακάτω εξισώσεις:

Για q = 6.75 έχουμε 2.5/q = 2.5/6.75 = 0.3703

0 ≤ T < 0.15: S_d (0) = 0.288·2/3 = 0.192, Sd(0.15) = 0.288·2.5/6.75 = 0.107 → και επομένως η ευθεία που ενώνει τα 2 σημεία (0.0, 0.192), (0.15, 0.0107) S_d(T) = 0.288·[2/3+T/0.15· (2.5/6.75-2/3)] = 0.192-0.569T

0.15 ≤ T < 0.50: καμπύλη S_d(T) = 0.107 → σταθερό σε όλο το εύρος

0.50 ≤ T < 2.50: καμπύλη S_d(T) = max ( γ _I · a_gR · S · 2.5/q[T_C/T], β · γ _I · a_gR) = max(0.107 · 0.50/T, 0.048) το σημείο καμπής στο Τ = 1.11 → δηλαδή μετά το Τ = 1.11 έχουμε ευθεία

2.50 ≤ T < 4.0: καμπύλη S_d(T) = max( max ( γ _I · a_gR · S · 2.5/q[T_CT_D/T²], β · γ _I · a_gR) = max(0.107 · 1.25/T², 0.048) το σημείο καμπής στο Τ = 1.67 → όλο είναι ευθύγραμμο τμήμα

Για q = 4.5 έχουμε 2.5/q = 2.5/4.5 = 25/45 = 0.555555556

0 ≤ T < 0.15: S_d (0) = 0.288 · 2/3 = 0.192, S_d(0.15) = 0.288 · 25/45 = 0.16 → και επομένως η ευθεία που ενώνει τα 2 σημεία (0.0, 0.192), (0.15, 0.16) Sd(T)=0.288· [2/3+T/0.15 · (2.5/4.5-2/3)] = 0.192-0.213T

0.15 ≤ T < 0.50: καμπύλη S_d(T) = 0.16 → σταθερό σε όλο το εύρος

0.50 ≤ T < 2.50: καμπύλη S_d(T) = max ( γ _I · a_gR · S · 2.5/q[T_C/T], β · γ _I · a_gR) = max(0.16 · 0.50/T, 0.048) το σημείο καμπής στο Τ = 1.67 → δηλαδή μετά το Τ = 1.67 έχουμε ευθεία

2.50 ≤ T < 4.0: καμπύλη S_d(T) = max( max ( γ _I · a_gR · S · 2.5/q[T_CT_D/T²], β · γ _I · a_gR) = max(0.16 · 1.25/T², 0.048) το σημείο καμπής στο Τ = 2.04 → όλο είναι ευθύγραμμο τμήμα

Για q = 3.0 έχουμε 2.5/q = 2.5/3.0 = 25/30 = 0.83333333333333

0 ≤ T < 0.15: S_d (0) = 0.288 · 2/3 = 0.192, S_d(0.15) = 0.288 · 0.83333333 = 0.24 → και επομένως η ευθεία που ενώνει τα 2 σημεία (0.0, 0.192), (0.15, 0.24) Sd(T)=0.288·[2/3+T/0.15 ·(2.5/3.0-2/3)] = 0.192+0.32T

0.15 ≤ T < 0.50: καμπύλη S_d(T) = 0.24 → σταθερό σε όλο το εύρος

0.50 ≤ T < 2.50: καμπύλη S_d(T) = max ( γ _I · a_gR · S · 2.5/q[T_C/T], β · γ _I · a_gR) = max(0.24 · 0.50/T, 0.048) το σημείο καμπής στο Τ = 2.5 → δεν υπάρχει ευθύγραμμο τμήμα

2.50 ≤ T < 4.0: καμπύλη S_d(T) = max( max ( γ _I · a_gR · S · 2.5/q[T_CT_D/T²], β · γ _I · a_gR) = max(0.24 · 1.25/T², 0.048)

το σημείο καμπής στο Τ = 2.5 → άρα όλο το τμήμα ευθεία στο 0.048

Για q = 1.5 έχουμε 2.5/q = 2.5/1.5 = 25/15 = 0.83333333333333

0 ≤ T < 0.15: S_d (0) = 0.288·2/3 = 0.192, S_d(0.15) = 0.288·1.66666666666667 = 0.48 → και επομένως η ευθεία που ενώνει τα 2 σημεία (0.0, 0.192), (0.15, 0.48) Sd(T)=0.288· [2/3+T/0.15· (2.5/1.5-2/3)] = 0.192+1.92T

0.15 ≤ T < 0.50: καμπύλη S_d(T) = 0.48 → σταθερό σε όλο το εύρος

0.50 ≤ T < 2.50: καμπύλη S_d(T) = max ( γ _I · a_gR · S · 2.5/q[T_C/T], β · γ _I · a_gR) = max(0.48 · 0.50/T, 0.048) το σημείο καμπής στο Τ = 5.0, → δηλαδή δεν υπάρχει ευθύγραμμο τμήμα

2.50 ≤ T < 4.0: καμπύλη S_d(T) = max( max ( γ _I · a_gR · S · 2.5/q[T_CT_D/T²], β · γ _I · a_gR) = max(0.48 · 1.25/T², 0.048) το σημείο καμπής στο Τ = 3.54 → άρα το τμήμα από Τ = 3.54 έως Τ = 4.0 ευθεία στο 0.048

Φάσμα σχεδιασμού κατακόρυφων σεισμικών δράσεων [EC8, §3.2.2.5(5)]

Στη μελέτη κτιρίων δεν είναι συνήθης η υποχρέωση να λαμβάνεται υπόψη η κατακόρυφη συνιστώσα του σεισμού (βλέπε §6.6.2) , όταν λαμβάνεται όμως υπόψη θα ισχύουν τα ακόλουθα:

• Χρησιμοποιείται το φάσμα σχεδιασμού της §6.1.6 όπου το a_g αντικαθίσταται από το a_vg = 0.9a_g [EC8, §3.2.3, πίνακας 3.4]

• Ο εδαφικός συντελεστής S λαμβάνεται ίσος με 1.0

• Ο συντελεστής q λαμβάνεται με τιμή q=1.5 ή και μικρότερη

Σε περίπτωση που υπάρχει σοβαρός λόγος, π.χ. πολυώροφα φυτευτά υποστυλώματα, επιβάλλεται να ληφθούν υπόψη οι κατακόρυφες σεισμικές επιταχύνσεις και ίσως ακόμη να ενδείκνυται να ληφθεί ενιαία τιμή q = 1.5 για όλον τον φορέα με την οποία θα γίνεται και ο υπολογισμός των οριζοντίων επιταχύνσεων..

Σε μία σοβαρή περίπτωση, είναι καλό να εξετασθεί ο φορέας παράλληλα με τη διαφραγματική λειτουργία και χωρίς αυτήν, τουλάχιστον στους κόμβους που υπάρχουν οι ιδιαιτερότητες, ώστε να προκύψει η ακριβής τιμή της κατακόρυφης σεισμικής επιτάχυνσης στους κρίσιμους κόμβους.

Για πρακτικούς λόγους και υπέρ της ασφαλείας, θα μπορούσε στους κρίσιμους κόμβους να λαμβάνεται η μέγιστη κατακόρυφη επιτάχυνση a_V που μπορεί να εμφανιστεί σε έναν κόμβο. Η μέγιστη αυτή κατακόρυφη σεισμική επιτάχυνση είναι a_V,max = 0.9·γ_I·a_gR·2.5/1.5 → a_V,max = 1.5·γ_I ·a_gR.