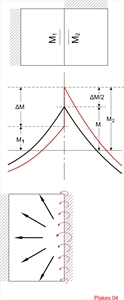
 Εικόνα 4.3.1
Εικόνα 4.3.1 Εικόνα 4.3.1 Μια κτιριακή κατασκευή διαθέτει συνήθως διάφορους τύπους πλακών (αμφιέρειστες, τριέρειστες, τετραέρειστες κ.λ.π.), οι οποίες μπορεί να μην είναι τυποποιημένες. Στην περίπτωση αυτή, κάθε πλάκα επιλύεται ξεχωριστά με τη χρήση πινάκων. Η ροπή M στην παρυφή (σύνορο) δύο πλακών είναι δυνατόν να λαμβάνεται ως ο μέσος όρος των εκατέρωθεν ροπών Μ1 (ροπή αριστερής πλάκας στην παρυφή) και Μ2 (ροπή δεξιάς πλάκας στην παρυφή).
Η διαφορά ΔΜ=M2-M1 ανακατανέμεται σε όλες τις διευθύνσεις των δύο πλακών, ενώ κατά κανόνα επηρεάζει λίγο τις υπόλοιπες ροπές στηρίξεων και ακόμη λιγότερο τις ροπές ανοιγμάτων. Ειδικές πλάκες (λοξές, όχι σταθερού πάχους κ.λ.π.) μπορεί να επιλυθούν με την αναγωγή τους σε ισοδύναμες ορθογωνικές σταθερού πάχους. Πλάτος εισαγωγής σημειακού φορτίου επί πλάκας 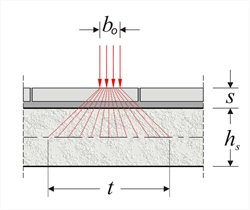 Εικόνα 4.3.2
Εικόνα 4.3.2 Εικόνα 4.3.2 Το πλάτος t εισαγωγής συγκεντρωμένου φορτίου P στο μέσο της πλάκας δίνεται από τη σχέση: t = b0 + 2 x (s+hs/2) = b0 + 2 x s + hs , όπου s το πάχοσ επικάλυψης Αν το σημειακό φορτίο εξασκείται απευθείας στην επιφάνεια του σκυροδέματος, όπως π.χ. στην περίπτωση τοιχοποιίας, δε λαμβάνεται υπόψη το πάχος s. Πλάτος διανομής σημειακού φορτίου 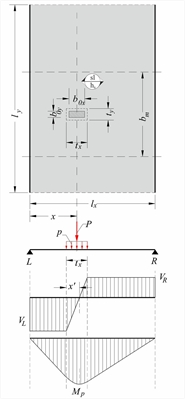 Εικόνα 4.3.3-1: Αμφιέρειστη πλάκα με συγκεντρωμένο φορτίο
Εικόνα 4.3.3-1: Αμφιέρειστη πλάκα με συγκεντρωμένο φορτίο Εικόνα 4.3.3-1: Αμφιέρειστη πλάκα με συγκεντρωμένο φορτίο Στην περίπτωση σημειακού, γραμμικού ή ομοιόμορφα κατανεμημένου φορτίου επί αμφιέρειστης πλάκας, εφόσον δεν πραγματοποιείται ακριβέστερη ανάλυση, το υπολογιστικό πλάτος bm διανομής του φορτίου καθορίζεται εγκάρσια στη διεύθυνση του κυρίου οπλισμού. Συμβολίζουμε με bm,fτο πλάτος διανομής της ροπής κάμψης του ανοίγματος, bm,s το πλάτος διανομής της ροπής κάμψης της στήριξης (εφόσον υπάρχει πακτωμένη στήριξη) και b m,v (bm,vL, bm,vR)το πλάτος διανομής της τέμνουσας (στην αριστερή και δεξιά στήριξη). Τα πλάτη αυτά, γενικά, διαφέρουν μεταξύ τους. Κάθε εντατικό μέγεθος aw σε κάθε θέση x oτης αμφιέρειστης πλάκας LR, λόγω του ομοιόμορφου φορτίουpd=γgxg+γqxq, διατηρείται σταθερό σε ολόκληρο το μήκος m διεύθυνσης y.Το συγκεντρωμένο φορίο P=γg xG+γqxQπροκαλεί πρόσθετο εντατικό μέγεθοςAP (σε μονάδες ροπής ή τέμνουσας) που αντιστοιχεί στο πλάτος διανομής BM,και επομένως ανά m διεύθυνσης y ισούται με aP=AP/bm Σύμφωνα με την αρχή της επαλληλίας, το συνολικό εντατικό μέγεθος που ασκείται στο τμήμα της πλάκας μήκους bm προκύπτει ίσο με atot=aw+aP,ενώ στο υπόλοιπο μήκος ly με aw. Το πλάτος διανομής συγκεντρωμένου φορτίου είναι συνάρτηση του είδους των στηρίξεων της πλάκας (πάκτωση, άρθρωση, ελεύθερη) και της απόστασης x του κέντρου βάρους του φορτίου από αυτές. Ο επόμενος πίνακας παραθέτει το πλάτος διανομής τμηματικά ομοιόμορφου φορτίου για κάθε είδος στήριξης.
Distribution width of partial uniform load | |
| b m , f = ty + 2.5 x x x (1-x/l) t x,max = l, t y,max = 0.8l | t x,max = l, t y,max = 0.8l b m , vR = t y + 0.5 x (l-x) t x,max = l, t y,max = 0.8l | | | bm,f=0.37+2.5x1.5x(1-0.375)=2.71 m | bm,vL=0.37+0.5x1.5=1.12 m bm,vR=0.37+0.5x2.5=1.62 m | | | bm,f=0.37+2.5x2.0x(1-0.5)=2.87 m | bm,vL=0.37+0.5x2.0=1.37 m bm,vR=0.37+0.5x2.0=1.37 m | | |
| b m , f = t y + 1.5 x x x (1-x/l) t x,max = l, t y,max = 0.8l b m ,s = t y + 0.5 x x x (2-x/l) t x,max = l, t y,max = 0.8l | t x,max = 0.2l, t y,max = 0.4l b m,vR = t y + 0.4 x (l-x) t x,max = 0.2l, t y,max = 0.4l | | | bm,f=0.37+1.5x1.5x(1-0.375)=1.78 m bm,s=0.37+0.5x1.5x(2-0.375)=1.59 m | bm,vL=0.37+0.3x1.5=0.82 m bm,vR=0.37+0.4x2.5=1.37 m | | | bm,f=0.37+1.5x2.0x(1-0.5)=1.87 m bm,s=0.37+0.5x2.0x(2-0.5)=1.87 m | bm,vL=0.37+0.3x2.0=0.97 m bm,vR=0.37+0.4x2.0=1.17 m | | |
| b m , f = t y + x x (1-x/l) t x,max = l, t y,max = 0.4l b m ,sL = t y + 0.5 x x x (2-x/l) b m ,sR = t y + 0.5 x (l-x) x (1+x/l) t x,max = l, t y,max = 0.4l | t x,max = 0.2l, t y,max = 0.4l b m ,vR = t y + 0.3 x (l-x) t x,max = 0.2l, t y,max = 0.4l | | | bm,f=0.37+1.5x(1-0.375)=1.31 m bm,sL=0.37+0.5x1.5x(2-0.375)=1.59 m bm,sR=0.37+0.5x2.5x(1+0.375)=2.09 m | bm,vL=0.37+0.3x1.5=0.82 m bm,vR=0.37+0.3x(4.0-1.5)=1.12 m | | | bm,f=0.37+2.0x(1-0.5)=1.37 m bm,s=0.37+0.5x2.0x(2-0.5)=1.87 m bm,sR=0.37+0.5x2.0x(1+0.5)=1.87 m | bm,vL=0.37+0.3x2.0=0.97 m bm,vR=0.37+0.3x(4.0-2.0)=0.97 m | | |
| t x,max = l, t y,max = 0.8l | t x,max = 0.2l, t y,max = 0.4l | | | | | | | | |
• Παρατήρηση: Ακολουθούν τα παραδείγματα 1 και 2. Παράδειγμα 1 (πλάκα στην αρχή της παραγράφου 3.3.1) 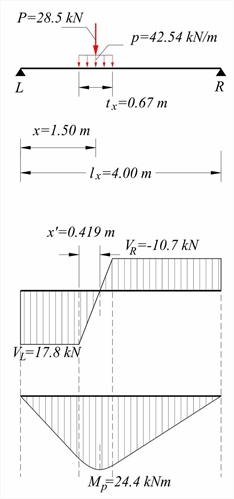 Εικόνα 4.3.3-2
Εικόνα 4.3.3-2 Εικόνα 4.3.3-2 Η πλάκα έχει διαστάσεις lx=4.00 m, ly=5.00 m και πάχος hs=170 mm. Καταπονείται από φορτίο επικάλυψης ge=1.0 kN/m2, ωφέλιμο q=5.0 kN/m2 και συγκεντρωμένο P (μόνιμο G=10.0 kN και κινητό Q=10.0 kN), το οποίο ασκείται απευθείας (s=0) στην πλάκα, έχει διαστάσεις b ox=0.50 m, boy=0.20 m και κέντρο βάρους σε απόσταση x=1.50 m από την αριστερή στήριξη. Οι στηρίξεις L,R είναι αρθρωτές. Ζητείται το διάγραμμα ροπών και τεμνουσών της πλάκας. Η επίλυση με τα ομοιόμορφα φορτία είναι ίδια με αυτή του παραδείγματος της §3.3.2 (vw=29.18 kN/m, mw=29.18 kNm/m). Η ένταση αυτή σχεδιασμού είναι ομοιόμορφη σε ολόκληρο το μήκος ly της πλάκας. Πλάτος εισαγωγής σημειακού φορτίου σχεδιασμού P P=1.35xG+1.50xQ=1.35x10.0+1.50x10.0=28.5 kN tx=box+hs=0.50+0.17=0.67 m ty=boy+hs=0.20+0.17=0.37 m Ισοδύναμο γραμμικά διανεμημένο φορτίο p στο txis p=P/tx=28.5kN/0.67m=42.5 kN/m Τέμνουσες δυνάμεις στις δύο στηρίξεις VL=Vx,L=pxtxx(lx-x)/lx=42.54x0.67x2.5/4.0=17.8 kN VR=Vx,R=Vx,L-pxtx=17.81-42.54x0.67=-10.7 kN Σημείο μηδενισμού τεμνουσών x'=VL/p=17.81kN/(42.54kN/m)=0.419 m Μέγιστη ροπή (βλέπε § 3.3.3, υποσημείωση 10) Πλάτη διανομής φορτίου (προηγούμενος πίνακας) tx,max=lx=4.0 m (>tx=0.67 m) και ty,max=0.8xlx=0.8x4.0=3.20 m (>ty =0.37 m) Η πρόσθετη ροπή σχεδιασμού στη ζώνη πλάτους bm,f=2.71 m ισούται με mP=MP/bm,f=24.48kNm/2.71m=9.03 kNm/m και η συνολική ροπή σχεδιασμού με mtot=mw+mP=29.18+9.03=38.21 kNm/m. Η πρόσθετη τέμνουσα σχεδιασμού στη ζώνη bm,vL=1.12 m ισούται με vP=VL/bm,vL=17.81kN/1.12m=15.9 kN/m και η συνολική τέμνουσα σχεδιασμού με vtot=vw+vP=29.2+15.9=45.1 kN/m. Εξετάζουμε την προηγούμενη πλάκα, στην οποία ασκείται πλέον συνεχές φορτίο g=8.0 kN/m λόγω τοιχοποιίας από L έως R (συνολικό φορτίο G=8.0kN/m * 4.00 m=32.0 kN) πάχους boy=0.20 m. Ζητείται το διάγραμμα ροπών και τεμνουσών της πλάκας. Η επίλυση με τα ομοιόμορφα φορτία είναι ίδια με αυτή του προηγούμενου παραδείγματος. Οι διαστάσεις του φορτίου ισούνται με box=4.00 m και boy=0.20 m. 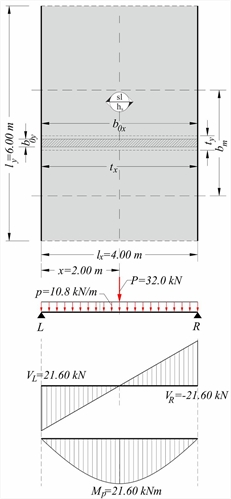 Εικόνα 4.3.3-3
Εικόνα 4.3.3-3 Εικόνα 4.3.3-3 Πλάτος εισαγωγής γραμμικού φορτίου σχεδιασμού p p=γgxg=1.35x8.0kN/m=10.8 kN/m tx=min(box+hs, lx)=min(4.00+0.17, 4.00)=4.00 m ty=boy+hs=0.20+0.17=0.37 m Τέμνουσες δυνάμεις στις δύο στηρίξεις VL=VR=pxlx/2=10.8x4.00/2=21.6 kN Mp=pxl2x/8=10.8x4.002/8=21.6 kNm. Πλάτη διανομής φορτίου (προηγούμενος πίνακας) ty,max=0.8xlx=0.8x4.00=3.20 m(>ty=0.37 m) bm,f=ty+2.5xxx(1-x/l)=0.37+2.5x2.00x(1-0.50) bm,vL=bm,vR=ty+0.5xx=0.37+0.5x2.00=1.37 m Η πρόσθετη ροπή σχεδιασμού στο πλάτος bm bm,f=2.87 m is equal to mp=Mp/bm,f=21.60kNm/2.87m=7.5 kNm/m και η συνολική ροπή σχεδιασμού με mtot=mw+mP=29.2+7.5=36.7 kNm/m. Η πρόσθετη τέμνουσα σχεδιασμού στη ζώνη πλάτους bm,vL=1.37 m is equal to vP=VL/bm,v=21.6kN/1.37m=15.8 kN/m while the total design shear force is equal to vtot=vw+vP=29.2+15.8= =45.0 kN/m. • Η πλάκα των δύο προηγούμενων παραδειγμάτων διαστασιολογείται σε κάμψη με ροπή mw=29.2 kNm/m (για ζώνη πλάτους 1.00 m). Ο αντίστοιχος οπλισμός a s,w (mm2/m)τοποθετείται ομοιόμορφα σε όλο το μήκος ly=6.00 m. • Το τμήμα m,f της πλάκας θα διαστασιολογηθεί σε κάμψη πάλι για ζώνη πλάτους 1.00 m με ροπή mtot, resulting to reinforcement as,tot (mm2/m). Ο πρόσθετος οπλισμός που απαιτείται για το τμήμα bm,f ισούται με as=as,tot-as,w (mm2/m) και As=asxbm,f (mm2),ενώ τοποθετείται σε ζώνη, συμμετρικά ως προς το φορτίο, πλάτους b zwith ty≤ bz ≤bm,f. ·• Πέραν του διαμήκους οπλισμού, απαιτείται και εγκάρσιος τόσο στην κάτω όσο και στην άνω ίνα της ζώνης, ίσος τουλάχιστον με το 60% του as και μήκους bm,f + μήκη αγκύρωσης. Αν επιλεγεί ζώνη π.χ. πλάτους bz=0.40 m,αυτή μπορεί να διαμορφωθεί σε μορφή κρυφοδοκού που θα συμβάλλει και στη στήριξη του άνω εγκάρσιου οπλισμού (Γ’ τόμος). Αυτό σημαίνει ότι η περιοχή διανομής οπλίζεται με μία λογική πλακοδοκού με πλάτος κορμού bz=0.40 m και πλάτος πλάκας bm,f. • Η πλάκα των δύο προηγούμενων παραδειγμάτων διαστασιολογείται με συνολική τέμνουσα v=45.1 kN για ζώνη πλάτους 1.00 m. 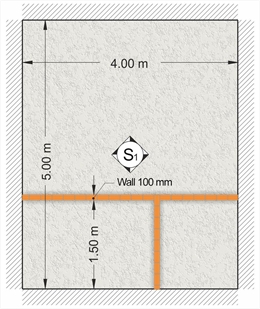 Εικόνα 4.3.3-4
Εικόνα 4.3.3-4 Εικόνα 4.3.3-4 Στην περίπτωση τετραέρειστης πλάκας, , τα σημειακά ή γραμμικά φορτία, γενικά κατανέμονται σε όλο το εμβαδόν της πλάκας υπό μορφή ομοιομορφισμένου φορτίου. Το φορτίο αυτό προστίθεται στα υπόλοιπα ομοιόμορφα φορτία της πλάκας Παράδειγμα : Δίνονται το ισοδύναμο ομοιόμορφο γραμμικό φορτίο τοίχου (δηλαδή το βάρος του τοίχου μείον το βάρος της πόρτας) του σχήματος στη διεύθυνση των 4.00 m ίσο με 5.0 kN/m και το εγκάρσιο φορτίο του συμπαγούς τοίχου ίσο με 6.0 kN/m. Ζητείται το ομοιομορφισμένο φορτίο των τοίχων στο σύνολο της επιφάνειας της πλάκας. 4.00mx5.0kN/m+1.50mx6.0kN/m=29.0 kN Ομοιομορφισμένο φορτίο τοίχων: 29.0kN/(4.00m x 5.00m)=1.45 kN/m2
|