|
« Διαφραγματική λειτουργία
Παραμορφώσεις-Εντάσεις »
|
Φορτιστικό προσομοίωμα σεισμού Υπάρχουν διάφορες μέθοδοι για την επίλυση ενός χωρικού πλαισίου σε σεισμό, άλλες περισσότερο και άλλες λιγότερο ακριβείς, όλες όμως προσεγγιστικές, όπως αναμένεται για ένα τόσο πολύπλοκο συνδυασμό γεωλογικών και δομικών αντικειμένων. Το βιβλίο “Αντισεισμικός Σχεδιασμός Κτιρίων από Οπλισμένο Σκυρόδεμα” τις περιγράφει αναλυτικά. Με τα σημερινά δεδομένα, που οι ηλεκτρονικοί υπολογιστές είναι ταχύτατοι, μία πολύ καλή λύση είναι η δυναμική φασματική μέθοδος με τη CQC μέθοδο υπολογισμού της περιβάλλουσας των εντατικών μεγεθών. Η μέθοδος της πλήρους τετραγωνικής επαλληλίας CQC έχει βέβαια το μειονέκτημα ότι τα εντατικά μεγέθη έχουν μόνο θετικό πρόσημο, που δυσχεραίνει τον προσδιορισμό των δυσμενέστερων συνδυασμών διαξονικής κάμψης, το οποίο όμως απαλύνεται με διάφορες προσεγγιστικές θεωρήσεις. Το εκπαιδευτικό λογισμικό που συνοδεύει το παρόν βιβλίο χρησιμοποιεί δύο τέτοιες μεθόδους, εκ των οποίων η πρώτη εφαρμόζει τη CQC για όλα τα εντατικά μεγέθη και τις παραμορφώσεις. Επειδή όλα τα εντατικά μεγέθη εξετάζονται και με το θετικό και με το αρνητικό πρόσημο (32 συνδυασμοί, βλέπε §6.5), η τελική λύση είναι ικανοποιητική. Υπάρχει και άλλη μία μέθοδος, η οποία υπερβαίνει το πρόβλημα του προσήμου, είναι απλή και παρέχει λογικά αποτελέσματα κλασικής στατικής (βλέπε §6.3.2). Λειτουργεί ως εξής: - Με βάση τις εδαφικές παραμέτρους του σεισμού, τη σεισμική επιτάχυνση του εδάφους, τις μάζες που ενεργοποιούνται κατά τη στιγμή του σεισμού στη θέση i και τη διαθέσιμη πλαστιμότητα του κτιρίου, υπολογίζουμε με CQC τις σεισμικές επιταχύνσεις αi,j(j=x,y,z) που εμφανίζονται σε κάθε θέση κατά X, Y, Z. Οι επιταχύνσεις αi,j λαμβάνουν πρόσημο από την κυρίαρχη ιδιομορφή (από την ιδιομορφή με τη μεγαλύτερη μάζα συμμετοχής).
- Υπολογίζουμε τις σεισμικές δυνάμεις Hi,j=ai,jxMi στη θέση i, ως το αλγεβρικό γινόμενο κάθε σεισμικής επιτάχυνσης επί τη μάζα της θέσης αυτής.
- Με βάση τις σεισμικές δυνάμεις Hi,j για κάθε σεισμικό συνδυασμό (π.χ. σεισμός κατά Y + 30%, σεισμός κατά X + 20%, σεισμός κατά Z) υπολογίζουμε τις σεισμικές εντάσεις κατά X, Y, Z.,
- Όταν ο σεισμικός συνδυασμός περιλαμβάνει τυχηματικές εκκεντρότητες (βλέπε §6.5), κάθε μάζα M ενός κόμβου i τοποθετείται στις συντεταγμένες του κόμβου i μετατεθειμένη με + ή – τις τυχηματικές εκκεντρότητες του ορόφου. Μ’ αυτό τον τρόπο αντιμετωπίζονται όλες οι περιπτώσεις των κόμβων, είτε ανήκουν στο διάφραγμα, είτε όχι. Αν όλοι οι κόμβοι ενός ορόφου ανήκουν στο διάφραγμα, η συνιστάμενη φόρτιση είναι ισοδύναμη με αυτή που θα προέκυπτε αν μεταθέταμε τη συνολική μάζα του ορόφου από το κέντρο μάζας κατά τις τυχηματικές εκκεντρότητες.
- Τα εντατικά μεγέθη κάθε συνδυασμού είναι προσημασμένα σύμφωνα με την κλασική στατική.
.jpg?bhow=0&w=500&h=500&Str=0) Εικόνα 3.2-1: Σεισμός κατά x: Υπολογισμός σεισμικών δυνάμεων με CQC όλων των ιδιομορφών
Εικόνα 3.2-1: Σεισμός κατά x: Υπολογισμός σεισμικών δυνάμεων με CQC όλων των ιδιομορφών Εικόνα 3.2-1: Σεισμός κατά x: Υπολογισμός σεισμικών δυνάμεων με CQC όλων των ιδιομορφών 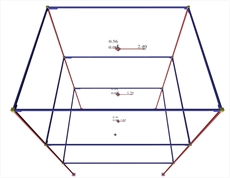 Εικόνα 3.2-2: Σεισμικές επιταχύνσεις
Εικόνα 3.2-2: Σεισμικές επιταχύνσεις
Εικόνα 3.2-2: Σεισμικές επιταχύνσεις
| 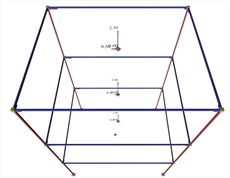 Εικόνα 3.2-3: Σεισμικές επιταχύνσεις
Εικόνα 3.2-3: Σεισμικές επιταχύνσεις
Εικόνα 3.2-3: Σεισμικές επιταχύνσεις
|
Το πλεονέκτημα της δεύτερης μεθόδου είναι ότι δίνει μεγέθη κλασικής στατικής κατανοητά στο μελετητή μηχανικό. Για παράδειγμα, οι σεισμικές επιταχύνσεις στους διαφραγματικούς ορόφους συμβατικών κτιρίων, πρέπει να ακολουθούν μία περίπου τριγωνική κατανομή με μηδενική τιμή στη βάση του κτιρίου και την επιτάχυνση σχεδιασμού ao στο κέντρο βάρους του. Το τρίγωνο αυτό υποδεικνύεται με κόκκινη διακεκομμένη γραμμή στο Interface του εκπαιδευτικού λογισμικού, προκειμένου ο μηχανικός να είναι σε θέση να ελέγξει την τάξη μεγέθους της κατανομής των σεισμικών επιταχύνσεων. Επίσης, με τη συγκεκριμένη μέθοδο δεν απαιτούνται επιπλέον δυναμικές φασματικές επιλύσεις. - Η κύρια σύγκριση πραγματοποιείται με τις σεισμικές επιταχύνσεις. Αυτό συμβαίνει διότι οι σεισμικές δυνάμεις παρέχουν το ίδιο ταχύ οπτικό αποτέλεσμα ως προς την καθ’ ύψος κατανομή τους, μόνο στην περίπτωση που οι μάζες των ορόφων είναι ίδιες.
- Όταν το κύριο σύστημα είναι υπό κλίση, για σεισμό μόνο κατά x, οι σεισμικές επιταχύν-σεις αναπτύσσονται και προς τις δύο διευθύνσεις x, y. Το ίδιο ισχύει και για σεισμό μόνο κατά y.
- Ο σεισμός κατά x δίνει συνιστώσες μόνο κατά x όταν η κατασκευή είναι συμμετρική, διαφορετικά δίνει συνιστώσες και κατά την άλλη διεύθυνση, όπως στο επόμενο παράδειγμα, που υπάρχει απόκλιση κέντρου ελαστικής στροφής και κέντρου μάζας.
| | | | | | | |
|
|
|
|
| Εικόνα 3.2-4: Δεκαώροφο κτίριο ασύμμετρουμικτού συστήματος (μελέτη B_547-3b) | Εικόνα 3.2-5: Κατανομή σεισμικών Επιταχύνσεων-Δυνάμεων-Τεμνουσών |
|
« Διαφραγματική λειτουργία
Παραμορφώσεις-Εντάσεις »
|

|