Έστω AB ράβδος πλάκας με μήκος L, ροπή αδράνειας I, μέτρο ελαστικότητας E, στην οποία ασκείται ομοιόμορφο φορτίο p. Με γνωστή την τέμνουσα VA,R (αριστερή στήριξη) και τη ροπή MA, ζητείται η εξίσωση της ελαστικής γραμμής λόγω κάμψης και το μέγιστο βέλος κάμψης. 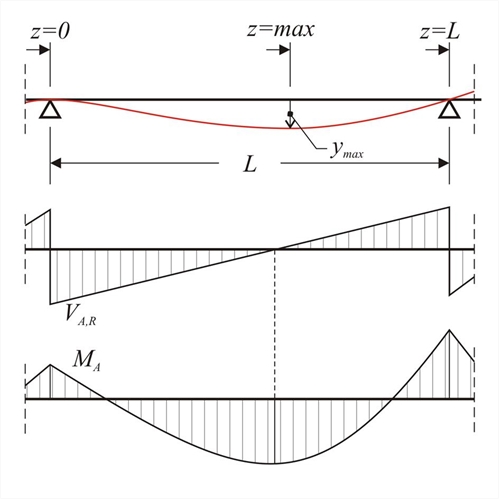 Εικόνα 4.5.2-1: Γενική περίπτωση κάμψης ράβδου (πλάκας ή δοκού)
Εικόνα 4.5.2-1: Γενική περίπτωση κάμψης ράβδου (πλάκας ή δοκού) Εικόνα 4.5.2-1: Γενική περίπτωση κάμψης ράβδου (πλάκας ή δοκού) Θεωρώντας ως αρχή των z το αριστερό άκρο της ράβδου έχουμε:
Η βασική εξίσωση της ελαστικής γραμμής επιλύεται σε δύο φάσεις:
Η εξίσωση της εφαπτομένης της ελαστικής γραμμής ισούται με:
Η εξίσωση της ελαστικής γραμμής ισούται τότε με:
Επομένως, η εξίσωση της εφαπτομένης της ελαστικής γραμμής (1) και η εξίσωση του βέλους κάμψης (2) είναι πλέον γνωστές. Η θέση στην οποία εμφανίζεται το μέγιστο βέλος κάμψης είναι το σημείο στο οποίο μηδενίζεται η πρώτη παράγωγος του, δηλαδή το σημείο z στο οποίο φ(z)=0.
Η συμβατή λύση της τριτοβάθμιας εξίσωσης (3) δίνει το ζητούμενο σημείο zmax, το οποίο αντικαθίσταται στην εξίσωση (2) και προκύπτει το μέγιστο βέλος κάμψης ymax.
Παράδειγμα: Βέλος κάμψης της πρώτης πλάκας (του παραδείγματος της §4.3.1): Για L=4.5 m, p=16.5 kN/m, VA,R=32.1 kN και MA=0.0, από την (3) προκύπτει ότι:
(4) > (16.5/6)·z3-(32.1/2)·z2-0+45.7=0 > 2.75z3-16.05z2+45.7=0 > z max=2.112 m (2) > Για πάχος πλάκας h=180 mm και μέτρο ελαστικότητας σκυροδέματος E=32.80 GPa έχουμε ότι: I=(b·h3)/12=(1.0x0.183)/12=486x10-6 m4 E·I=32.8x109N/m2x486x10-6m4=15.9408x106 N·m2, therefore,
Παράδειγμα: Βέλος κάμψης της δεύτερης πλάκας (του παραδείγματος της §4.3.1): Για L=4.0 m, p=9.75 kN/m, VA,R=21.7 kN και MA=-22.6 kNm, από την (3) προκύπτει ότι:
(4) > (9.75/6)·z3-(21.7/2)·z2+22.6z-13.333=0 > 1.625z3-10.85z2+22.6z-13.333=0 > zmax=0.993m
Για πάχος πλάκας h=140 mm και μέτρο ελαστικότητας σκυροδέματος E=32.80 GPa έχουμε ότι: I=(b·h3)/12=1.0x0.143/12=228.7x10-6 m4 E·I=32.8x109N/m2x228.7x10-6m4=7.5014x106 N·m, therefore,
Παράδειγμα: Βέλος κάμψης της τρίτης πλάκας (του παραδείγματος της §4.3.1): Για L=4.0 m, p=9.75 kN/m, VA,R=23.0 kN και MA=-13.9 kNm, από την (3) προκύπτει ότι: C1=(-9.75x4.03/24+23.0x4.02/6-13.9x4.0/2) kN·m2 =7.533 kN·m2 (4) > (9.75/6)·z3-(23.0/2)·z2+13.9z+7.533=0 a 1.625z3-11.50z2+13.9z+7.533=0 a zmax=2.181m
Για πάχος πλάκας h=140 mm και για μέτρο ελαστικότητας σκυρόδεματος E=32.80 GPa: I=(b·h3)/12=1.0x0.143/12=228.7x10-6 m4 E·I=32.8x109N/m2x228.7x10-6m4=7.5014x106 N·m2, άρα,
Η ελαστική γραμμή της συνεχούς πλάκας που προκύπτει από τις εξισώσεις (1.2), (2.2), (3.2) είναι η ακόλουθη: .jpg?bhow=0&w=500&h=500&Str=0) Εικόνα 4.5.2-2: Η ελαστική γραμμή από τις εξισώσεις των 3 πλακών
Εικόνα 4.5.2-2: Η ελαστική γραμμή από τις εξισώσεις των 3 πλακών Εικόνα 4.5.2-2: Η ελαστική γραμμή από τις εξισώσεις των 3 πλακών
Η μελέτη (pi-FES) εξάγει τις ταυτόσημες παραμορφώσεις:  Εικόνα 4.5.2-3: Η ελαστική γραμμή από το pi-FES (Ενεργό module\SLABS) σε όψη
Εικόνα 4.5.2-3: Η ελαστική γραμμή από το pi-FES (Ενεργό module\SLABS) σε όψη Εικόνα 4.5.2-3: Η ελαστική γραμμή από το pi-FES (Ενεργό module\SLABS) σε όψη
|