Οι αμφιέρειστες πλάκες στηρίζονται σε δύο απέναντι παρυφές, όπως η s1 στην εικόνα της §4.1.
Αν μία αμφιέρειστη πλάκα στηρίζεται επιπρόσθετα σε μία ή δύο ακόμη παρυφές και ο λόγος του μεγαλύτερου προς το μικρότερο θεωρητικό άνοιγμα είναι μεγαλύτερος του 2.0 (πλάκα s3 στην ίδια εικόνα), υπολογίζεται ως αμφιέρειστη προς την κύρια διεύθυνση, ενώ λαμβάνονται υπ' όψη και οι δευτερεύουσες εντάσεις στις υπόλοιπες παρυφές.
Οι συνεχείς αμφιέρειστες πλάκες επιλύονται με τη θεώρηση συνεχούς ραβδωτού φορέα, του οποίου κάθε ράβδος έχει ορθογωνική διατομή πλάτους 1.00 m και ύψους όσο το πάχος της πλάκας. Οι λωρίδες φορτίζονται με τα ίδια βάρη, τα μόνιμα και τα κινητά φορτία που εξασκού-νται σ' αυτές.
Η επίλυση πραγματοποιείται:
α) προσεγγιστικά με την εφαρμογή του συνόλου των φορτίων σχεδιασμού p=1.35g+1.50q (όταν το κινητό φορτίο είναι σχετικά μικρό)
β) είτε με ακρίβεια λαμβάνοντας δυσμενείς φορτίσεις.
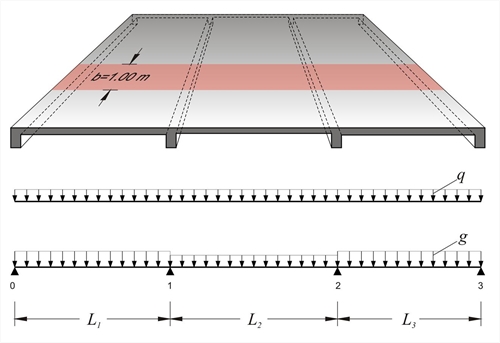 Εικόνα 4.5.1-1: Συνεχής πλάκα τριών ανοιγμάτων
Εικόνα 4.5.1-1: Συνεχής πλάκα τριών ανοιγμάτων Εικόνα 4.5.1-1: Συνεχής πλάκα τριών ανοιγμάτων
Οι 3 πλάκες (προηγούμενο σχήμα) έχουν L1=4.50 m, h1=180 mm, g1=10.0 kN/m2, q1=2.0 kN/m2, L2=4.00 m, h2=140 mm, g2=5.0 kN/m2, q2=2.0 kN/m2, L3=4.00 m, h3=140 mm, g3=5.0 kN/m2, q3=2.0 kN/m2, όπου τα φορτία g περιλαμβάνουν και το ίδιο βάρος. Ζητείται η στατική επίλυση των πλακών θεωρώντας καθολική φόρτιση για κατάσταση αστοχίας.
Το φορτίο σχεδιασμού σε κάθε πλάκα ισούται με pi=γgxgi+γqxqi=1.35 xgi+1.50xqi, οπότε σε ζώνη πλάτους 1.00 m ισχύει ότι:
p1=1.35x10.0+1.50x2.0=16.5 kN/m
p2=p3=1.35x5.0+1.50x2.0=9.75 kN/m
Η συνεχής πλάκα 3 ανοιγμάτων θα υπολογισθεί με τη μέθοδο Cross.
Θεμελιώδεις ροπές ανοιγμάτων (πίνακας b3)
M10=-p1xL12/8=-16.5x4.502/8=-41.8 kNm
M12=M21=-p2xL22/12=-9.75x4.002/12=-13.0 kNm
M23=-p3xL32/8=-9.75x4.002/8=-19.5 kNm
I01=Ic=1.0x0.183/12=4.86x10-4 m4
I12=I23=1.0x0.143/12=2.29x10-4 m4=0.47Ic
Συντελεστές δυσκαμψίας k, δείκτες κατανομής υ