Η §4.2.3 περιγράφει τη γενική περίπτωση των δυσμενών φορτίσεων για κάθε είδους πλάκα. Στην παράγραφο αυτή εξειδικεύεται η υποβολή και ο τρόπος υπολογισμού δυσμενών φορτίσεων στην ειδική περίπτωση συμμετρικής ομάδας τετραέρειστων πλακών.
Οι δυσμενείς φορτίσεις είναι πάντοτε ζατρικοειδούς μορφής. Η ιδιότητα αυτή μας οδηγεί στη θεώρηση δύο ισοδύναμων φορτίσεων, μίας με ομοιόμορφα κατανεμημένα θετικά φορτία του ιδίου μεγέθους και μίας άλλης ζατρικοειδούς μορφής με ομοιόμορφα κατανεμημένα φορτία ίσου μεν μεγέθους, εναλλασσόμενου δε προσήμου.
Το τέχνασμα αυτό υλοποιείται στο ακόλουθο παράδειγμα. Αξίζει να σημειώσουμε ότι η παράγραφος των ασκήσεων του κεφαλαίου αυτού ασχολείται με την επίλυση μεγάλης ομάδας τετραέρειστων συμμετρικών πλακών.
Ζητούνται οι ροπές αστοχίας των πλακών του σχήματος οι οποίες φέρουν φορτία επικάλυψης gεπ=1.5 kN/m2 και ωφέλιμο a) q= 2.0 kN/m2, b) 5.0 kN/m2, c) 10.0 kN/m2.
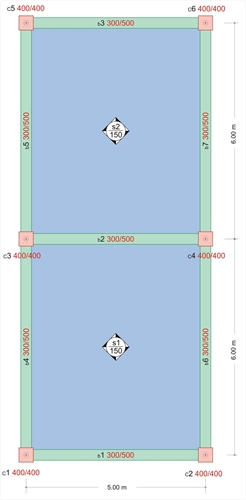Εικόνα 4.6.4-1 : Μελέτη <Β_464> Εικόνα 4.6.4-1 : Μελέτη <Β_464>
Για τον υπολογισμό της δυσμενέστερης ροπής στηρίξεως, οι δύο πλάκες φορτίζονται με το σύνολο των φορτίων:
Για τον υπολογισμό των μέγιστων και ελάχιστων ροπών στα δύο ανοίγματα, η μια πλάκα φορτίζεται με το ελάχιστο φορτίο σχεδιασμού gd=g και η άλλη με το μέγιστο pd=1.35g+1.50q.
Θεωρούμε τις 2 ακόλουθες ανεξάρτητες φορτίσεις p1 and p2
Το μόνιμο φορτίο ισούται με:
g=0.15x25.0+1.5=5.25 kN/m2, οπότε για
a) Για ωφέλιμο φορτίο q=2.0 kN/m2
p1=5.25+(0.35x5.25+1.5x2.0)/2= =5.25+2.42=7.67 kN/m2
p2=(0.35g+1.50q)/2=2.42 kN/m2 >
gd=p1-p2=5.25 & pd=p1+p2=10.09 kN/m2
b) Για ωφέλιμο φορτίο q=5.0 kN/m2
p1=5.25+(0.35x5.25+1.5x5.0)/2= =5.25+4.67=9.92 kN/m2,
p2=(0.35g+1.50q)/2=4.67 kN/m2 >
gd=p1-p2=5.25 & pd=p1+p2=14.59 kN/m2
c) Για ωφέλιμο φορτίο q=10.0 kN/m2
p1=5.25+(0.35x5.25+1.5x10.0)/2= =5.25+8.42=13.67 kN/m2
p2=(0.35g+1.50q)/2=8.42 kN/m2 >
gd=p1-p2=5.25 & pd=p1+p2=22.09 kN/m2
Κάθε πλάκα επιλύεται για δύο είδη στηρίξεων χρησιμοποιώντας τους ανάλογους συντελεστές για
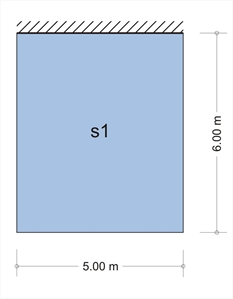Εικόνα 4.6.4-2 Εικόνα 4.6.4-2
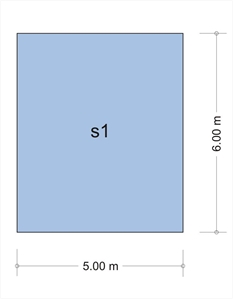Εικόνα 4.6.4-3 Εικόνα 4.6.4-3
Ο πίνακας b5.2 δίνει για πλάκα s1 (μία πακτωμένη παρυφή, αρθρωτές οι υπόλοιπες τρεις) kx,1=0.453, ky,1=0.547, vx,1=0.738, v y,1=0.631, ενώ ο πίνακας b5.1 δίνει για την πλάκα s1 (αρθρωτές και οι τέσσερις παρυφές) kx,2=0.675, ky,2=0.325, vx,2=vy,2=0.610.
Η δυσμενέστερη ροπή της στήριξης προκύπτει με τη μέγιστη φόρτιση pd και των δύο πλακών. Τόσο η γεωμετρία όσο και η φόρτιση είναι συμμετρικές, οπότε η στατική λειτουργία των δύο πλακών είναι ακριβώς η ίδια και επομένως η ροπή στήριξης s1-s2 είναι ίση με τη ροπή πάκτωσης κάθε μίας.
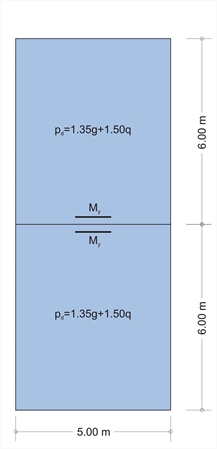Εικόνα 4.6.4-4 Εικόνα 4.6.4-4 |
a) Για ωφέλιμο φορτίο q= 2.0 kN/m2
b) Για ωφέλιμο φορτίο q= 5.0 kN/m2
c) Για ωφέλιμο φορτίο q= 10.0 kN/m2
|
Η μέγιστη ροπή κάθε ανοίγματος προκύπτει με φόρτιση του ενός ανοίγματος με pd και του άλλου με gd. Oπως φαίνεται στο πρώτο από τα τρία ακόλουθα σχήματα. Οι φορτίσεις αυτές είναι ισοδύναμες με pd=p1+p2 και gd=p1-p2 αντίστοιχα. Η επίλυση πραγματοποιείται με τις ισοδύναμες φορτίσεις p1 and p2.
Οι πρώτες ισοδύναμες φορτίσεις είναι συμμετρικές, οπότε και οι δύο πλάκες λειτουργούν με τη μία παρυφή πλήρως πακτωμένη και τις τρεις άλλες παρυφές αρθρωτές. Οι δεύτερες ισοδύναμες φορτίσεις είναι αντι-συμμετρικές, οπότε και οι δύο πλάκες λειτουργούν με τις τέσσερις παρυφές τους πλήρως αρθρωτές. Επομένως οι 2 επιμέρους επιλύσεις θα είναι ακριβείς, όπως και η συνισταμένη τους.
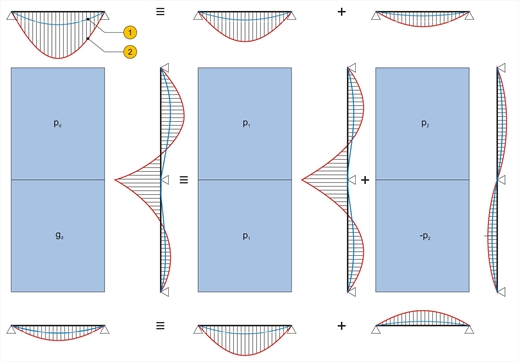Εικόνα 4.6.4-5 Εικόνα 4.6.4-5
(1) ελαστική γραμμή, (2) διάγραμμα ροπών