Θεμελιώδεις ροπές στήριξης και ροπές ανοιγμάτων – Βέλη κάμψης Δύο από τις μεθόδους υπολογισμού είναι: η μέθοδος Marcus και η μέθοδος Czerny. Σ' αυτήν, η πλάκα αντικαθίσταται από δύο διασταυρούμενες λωρίδες κατά τις διευθύνσεις x και y, οι οποίες συναντώνται στο μέσον m της πλάκας. Ανάλογα με τις συνθήκες στήριξης, οι λωρίδες διακρίνονται σε αμφιαρθρωτές, μονόπακτες ή αμφίπακτες. Κάθε λωρίδα με το αντίστοιχο φορτίο της δίνει μία ελαστική γραμμή και ένα διάγραμμα ροπών: 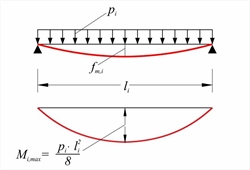 Εικόνα 4.6.1.2-1 :Αμφιαρθρωτή λωρίδα πλάκας
Εικόνα 4.6.1.2-1 :Αμφιαρθρωτή λωρίδα πλάκας Εικόνα 4.6.1.2-1 :Αμφιαρθρωτή λωρίδα πλάκας
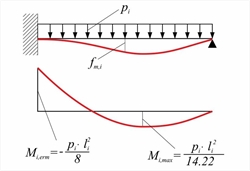 Εικόνα 4.6.1.2-2 : Μονόπακτη λωρίδα πλάκας
Εικόνα 4.6.1.2-2 : Μονόπακτη λωρίδα πλάκας Εικόνα 4.6.1.2-2 : Μονόπακτη λωρίδα πλάκας
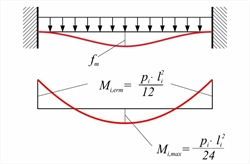 Εικόνα 4.6.1.2-3 : Αμφίπακτη λωρίδα πλάκας
Εικόνα 4.6.1.2-3 : Αμφίπακτη λωρίδα πλάκας Εικόνα 4.6.1.2-3 : Αμφίπακτη λωρίδα πλάκας
Κάθε λωρίδα παραλαμβάνει φορτίο px ή py τέτοιο ώστε:
Από τις εξισώσεις (1) και (2) υπολογίζονται τα φορτία px=kx·p και py=ky·p (kx+ky=1.00) όπου:
[*] Notef0m=cx·px·l4x/(E·I)=12·cx·kx·l4x/(E·b·h3)=aom·l4x/(E·1.0·h3), όπου a om=12·cx·kx Notef0m=cx·px·l4x/(E·I)=12·cx·kx·l4x/(E·b·h3)=aom·l4x/(E·1.0·h3), όπου a om=12·cx·kx
Οι ροπές ανοιγμάτων και στηρίξεων υπολογίζονται με την επίλυση αρθρωτών, μονόπακτων ή αμφίπακτων λωρίδων υπό φορτίο px και py κατά τις δύο διευθύνσεις αντίστοιχα. Η θεώρηση των ανεξάρτητων διασταυρούμενων λωρίδων δε λαμβάνει υπόψη τη συνεργασία τους με τις γειτονικές μέσω των ροπών συστροφής. Η ευνοϊκή επίδραση των ροπών συστροφής στις ροπές των ανοιγμάτων δίνεται με τους συντελεστές συστροφής νi (i=x, y),όπου:
Οι ροπές συστροφής επηρεάζουν μόνο τις ροπές ανοιγμάτων.
Όταν η πλάκα δε συνδέεται μονολιθικά στα σημεία έδρασής της, υπάρχουν συναντώμενες ελεύθερες παρυφές και δεν προβλέπεται οπλισμός συστροφής, οι ροπές των ανοιγμάτων προκύπτουν μεγαλύτερες, δηλαδή:
Οι εξισώσεις για τις έξι περιπτώσεις τετραέρειστων πλακών εξειδικεύονται ανάλογα με το είδος των στηρίξεων. Ενδεικτικά, υπολογίζονται οι συντελεστές για 3 λόγους πλευρών:
Τύπος 1 (αρθρωτή έδραση των τεσσάρων παρυφών)
Για ε=1.0: kx=0.500, ky=0.500, νx=0.583, νy=0.583, 100am=4.55 (against 4.87) Για ε=3/2: kx=0.835, ky=0.165, νx=0.691, νy=0.691, 100am=9.02 (against 9.27) Τύπος 2 (πλήρης πάκτωση μίας παρυφής, ελεύθερη έδραση των τριών άλλων)
Για ε=2/3: kx=0.073, ky=0.927, νx=0.863, νy=0.807, 100am=0.98 (against 4.98/1.54=0.98) Για ε=1.0: kx=0.286, ky=0.714, νx=0.762,νy=0.665, 100am=3.41 (against 3.34) Για ε=3/2: kx=0.669, ky=0.331, νx=0.752, νy=0.651, 100am=7.86 (against 7.73) Τύπος 3(πλήρης πάκτωση δύο απέναντι παρυφών, ελεύθερη έδραση των δύο άλλων)
Για ε=2/3: kx=0.038, ky=0.962, νx=0.929, νy=0.881, 100am=0.55 (against 2.97/1.54=0.59) Για ε=1.0: kx=0.167, ky=0.833, νx=0.861, νy=0.769, 100am=2.25 (against 2.30) Για ε=3/2: kx=0.503, ky=0.497, νx=0.814, νy=0.690, 100am=6.40 (against 6.39) Τύπος 4 (πλήρης πάκτωση δύο γειτονικών παρυφών και ελεύθερη έδραση των δύο άλλων)
Για ε=2/3: kx=0.165, ky=0.835, νx=0.826, νy=0.826, 100am=0.85 (against 4.59/1.54=0.91) Για ε=1.0: kx=0.500, ky=0.500, νx=0.765, νy=0.765, 100am=2.39 (against 2.52) Για ε=3/2: kx=0.835, ky=0.165, νx=0.826, νy=0.826, 100am=4.31 (against 4.59) Τύπος 5 (πλήρης πάκτωση τριών παρυφών και ελεύθερη έδραση της τέταρτης)
Για ε=2/3: kx=0.090, ky=0.910, νx=0.905, νy=0.888, 100am=0.51 (against 2.9/1.54=0.57) Για ε=1.0: kx=0.333, ky=0.667, νx=0.844, νy=0.815, 100am=1.76 (against 1.88) Για ε=3/2: kx=0.717, ky=0.283, νx=0.850, νy=0.823, 100am=3.81 (against 4.09) Τύπος 6 (πλήρης πάκτωση των τεσσάρων παρυφών)
Για ε=2/3: kx=0.165, ky=0.835, νx=0.897 και νy=0.897, 100am=0.46 (against 2.64/1.54=0.52) Για ε=1.0: kx=0.500, ky=0.500, νx=0.861 και νy=0.861, 100am=1.35 (against 1.52) Για ε=3/2: kx=0.835, ky=0.165, νx=0.897 και νy=0.897, 100am=2.34 (against 2.64) -
Σε περίπτωση δοκιδωτής (Zoellner) πλάκας, ο υπολογισμός των ροπών και του βέλους κάμψης, γίνεται προσεγγιστικά με τη χρήση μειωμένων συντελεστών νx, νy ίσων με ν'x, ν'y, ή ακόμη και με τιμή ίση με 1.0. -
Για τον υπολογισμό του βέλους κάμψης χρησιμοποιείται η πραγματική ροπή αδράνειας I της δοκιδωτής πλάκας, η οποία προκύπτει με τον πολλαπλασιασμό της τιμής των πινάκων επί το μειωτικό συντελεστή Ι/(1.0-h3/12)<1.0.
Μέθοδος ελαστικότητας κατά CZERNY
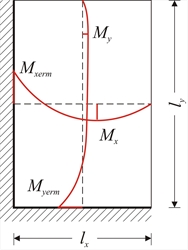 Εικόνα 4.6.2.2
Εικόνα 4.6.2.2 Εικόνα 4.6.2.2 Ανάλογα με το λόγο ε = lx / ly (όπου lx η μικρότερη διάσταση) και τον τύπο της στήριξης, από τους πίνακες της §4.6.1.2, προκύπτουν συντελεστές που δίνουν τις ροπές των ανοιγμάτων και των στηρίξεων των πλακών. Ισχύει ότι:
-
Οι ροπές και οι τέμνουσες στη μέθοδο Czerny εκφράζονται σε συνάρτηση με τη μικρότερη διάσταση lx σε αντίθεση με τη μέθοδο Marcus, στην οποία η ροπή κάθε διεύθυνσης είναι συνάρτηση της διάστασης της διεύθυνσης αυτής. -
Οι πίνακες των πλακών αναφέρονται συνήθως σε λόγους πλευρών ly/lx≥1.Όταν ly/lx<1, η πλάκα θεωρείται με στροφή 90 ο. -
Σε ορισμένους πίνακες δίνονται και οι ροπές συστροφής Mxy (όταν φυσικά υπάρχουν οι προϋποθέσεις εμφάνισης τους), καθώς και οι τέμνουσες δυνάμεις για περιπτώσεις κάμψης, με ή χωρίς ροπές συστροφής στις παρυφές.
|