Επιρροή κάμψης και διάτμησης σε παραμορφώσεις και εντάσεις Από τη μηχανική είναι γνωστό ότι η παραμόρφωση ενός μέλους εξαρτάται από τα έργα των ρο-πών κάμψης και των τεμνουσών δυνάμεων. Η δυσκαμψία E ·I των διατομών των αντισεισμικών στοιχείων (ρηγματωμένες διατομές) λαμβάνεται ίση με το 50% των αντίστοιχων αρηγμάτωτων [EC8, §4.3.1(6),(7)]. Το μέτρο διάτμησης G, από το οποίο εξαρτάται η διατμητική παραμόρφωση, συνδέεται με το μέτρο ελαστικότητας E και το συντελεστή Poisson ν με την ακόλουθη σχέση, Ο EC2 θεωρεί για ρηγματωμένη διατομή ν=0 και για αρηγμάτωτη διατομή ν=0.2 → το G κυμαίνεται από 0.5E έως 0.42E. Για αντισεισμικούς υπολογισμούς συνιστάται να λαμβάνεται ν=0 και επομένως G=0.5E. Ας εξετάσουμε ένα απλό υποστύλωμα που είναι πακτωμένο στη βάση και στην κορυφή του και φέρει στην κεφαλή του μάζα m. Η επιτάχυνση της βαρύτητας δίνει ένα κατακόρυφο φορτίο W=g·m. Λόγω της σεισμικής επιτάχυνσης α, αναπτύσσεται οριζόντια δύναμη H=a·m[=(a/g)·W στην κεφαλή του υποστυλώματος, η οποία μετατοπίζεται κατά δ σε σχέση με τον πόδα του.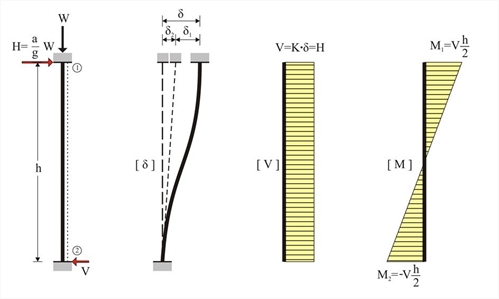 
Εικόνα 5.1.1: Αμφίπακτο υποστύλωμα: K = (12 E I / h 3) k va Εικόνα 5.1.1: Αμφίπακτο υποστύλωμα: K = (12 E I / h 3) k va
Η συνολική παραμόρφωση δ οφείλεται: ((α) στην παραμόρφωση δ1 λόγω της κάμψης που προκαλεί η δύναμη H, για την οποία ισχύει
(β) στην παραμόρφωση δ2 λόγω της διάτμησης που προκαλεί η δύναμη H, για την οποία ισχύει
όπου kz είναι ο συντελεστής διόρθωσης της επιρροής της τέμνουσας, G είναι το μέτρο διάτμησης του σκυροδέματος και A η διατομή του σκυροδέματος.
Συνοψίζοντας, η οριζόντια σεισμική δύναμη Η συνδέεται μέσω της ακόλουθης σχέσης με την αντίστοιχη μετατόπιση δ:
Ο όρος K ονομάζεται δυσκαμψία της αμφίπακτης κολόνας. Ο συντελεστής kva καλείται διορθωτικός συντελεστής της καμπτικής δυσκαμψίας της αμφίπακτης κολόνας λόγω διάτμησης. Ισχύει πάντα kva<1.0. Για συνήθη υποστυλώματα μπορεί να αγνοείται δηλαδή λαμβάνεται ίσος με kva=1.0), ενώ για τοιχία πρέπει να λαμβάνεται υπόψη το ενώ για τοιχία πρέπει να λαμβάνεται υπόψη το kva επειδή η τιμή του είναι σημαντικά μικρότερη της μονάδας. Ενδεικτικά για τοιχία με μήκος της τάξης του 1.0 m έχουμε kva≈0.80, ενώ για τοιχία με μήκος της τάξης των 2.0 m ισχύει kva≈0.50. Δίνεται αμφίπακτο υποστύλωμα διατομής 400mm/400mm, ύψος h=3.0m, μέτρο ελαστικότητας E=32.8GP, συγκεντρωμένη μάζα στην κεφαλή του m=80t, συντελεστής σεισμικής επιτάχυνσης σχεδιασμού στην κεφαλή του υποστυλώματος a/g=0.10. Ζητούνται τα εντατικά μεγέθη της κολόνας και η μετατόπιση της κεφαλής της σε σχέση με τον πόδα W=80·1000kg·10m/sec2=800 kN, H=0.10·800=80 kN, V=H=80 kN M1=-Μ2=-H·h/2=-80·3.0/2=120 kNm, I=0.40·0.403/12=21.33·10-4 m4 Αν δε ληφθεί υπόψη η διάτμηση, K=12·EI/h3=12·32.8·109·Ν/m2·21.33·10-4m4/(3.03·m3)=31.10·106 N/m Αν ληφθεί υπόψη η διάτμηση, επειδή G=0.5E, kz=5/6 (ορθογωνική διατομή) και A=b·d:
Η σχέση αυτή είναι ανεξάρτητη του πλάτους της διατομής και ισχύει για κάθε αμφίπακτη κολόνα ορθογωνικής διατομής. Για το συγκεκριμένο υποστύλωμα είναι
K = (E· I / h3)· Kva =31.10·106·0.959 N/m =29.82·106 N/m. Αν δεν ληφθεί υπόψη η διάτμηση, δ=H/K=80·103N/(31.10·106N/m) =2.57 mm. Αν ληφθεί υπόψη η διάτμηση, δ=H/K=80·103N/(29.82·106N/m) =2.68 mm, δηλαδή σ’ αυτή την περίπτωση η μετακίνηση προκύπτει μεγαλύτερη κατά 4% σε σχέση με την περίπτωση που δεν ληφθεί υπόψη η διάτμηση.
Τα ίδια δεδομένα και τα ίδια ζητούμενα για τοιχίο διατομής 2000/300. W=80·1000kg·10m/sec2=800 kN, H=0.10·800=80 kN, V=H=80 kN M1=-Μ2=-H·h/2=-80·3.0/2=120 kNm, I=0.30·2.003/12=0.20 m4 Αν δεν ληφθεί υπόψη η διάτμηση, K=12·EI/h3=12·32.8·109·Ν/m2·0.20m4/(3.03·m3)=2915.56·106 N/m Για το συγκεκριμένο υποστύλωμα είναι
και επομένως K = (E· I / h3)· Kva =2915.56·106·0.484 N/m =1410.75·106 N/m Αν δεν ληφθεί υπόψη η διάτμηση, δ=H/K=80·103N/(2915.56·106N/m) =0.027 mm. Αν ληφθεί υπόψη η διάτμηση, δ=H/K=80·103N/(1410.75·106N/m) =0.057 mm, δηλαδή σ’ αυτή την περίπτωση η μετακίνηση προκύπτει μεγαλύτερη κατά 110% σε σχέση με την περίπτωση που δεν ληφθεί υπόψη η διάτμηση. |