Επιρροή κινητού φορτίου στη στατική επίλυση αμφιέρειστων πλακών Η ακριβής επίλυση μίας συνέχειας αμφιέρειστων πλακών πραγματοποιείται με την επαλληλία των ακόλουθων φορτίσεων (δυσμενείς φορτίσεις). Επίλυση με τα ελάχιστα μόνιμα φορτία σχεδιασμού gd,i=1.0gi  Εικόνα 4.5.3.1-1
Εικόνα 4.5.3.1-1 Εικόνα 4.5.3.1-1 Μέγιστες και Ελάχιστες ροπές ανοιγμάτων (φόρτιση εναλλάξ των ανοιγμάτων) 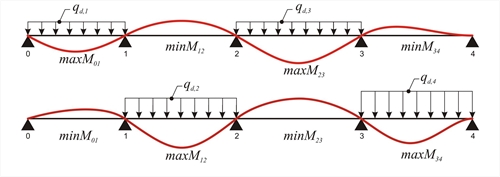 Εικόνα 4.5.3.1-2
Εικόνα 4.5.3.1-2 Εικόνα 4.5.3.1-2 Ελάχιστες ροπές στηρίξεων (φόρτιση παρακείμενων ανοιγμάτων και εναλλάξ των υπολοίπων) 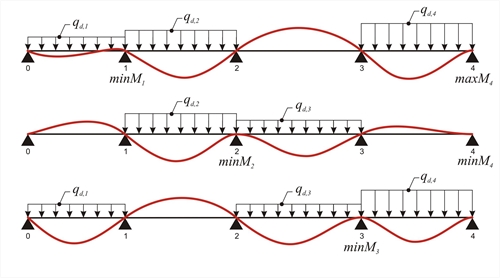 Εικόνα 4.5.3.1-3
Εικόνα 4.5.3.1-3 Εικόνα 4.5.3.1-3 Μέγιστες ροπές στηρίξεων (κενή φόρτιση παρακείμενων ανοιγμάτων και εναλλάξ των υπολοίπων) 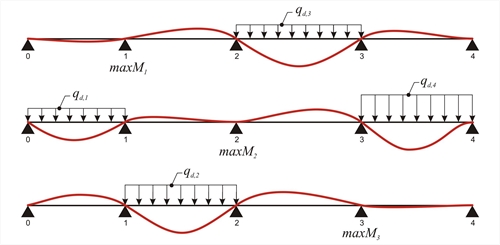 Εικόνα 4.5.3.1-4
Εικόνα 4.5.3.1-4 Εικόνα 4.5.3.1-4 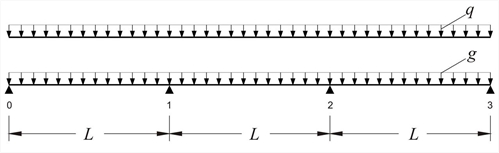 Εικόνα 4.5.3.1-5
Εικόνα 4.5.3.1-5 Εικόνα 4.5.3.1-5 Η συνεχής πλάκα του σχήματος έχει σε κάθε άνοιγμα μήκος L=5.00 m και πάχος h=160 mm, ενώ καταπονείται από φορτίο επικάλυψης ge=1.0 kN/m 2 και ωφέλιμο q=5.0 kN/m2. Σκρόδεμα C50/60.Ζητείται η περιβάλλουσα των ροπών και των τεμνουσών, σε οριακή κατάσταση αστοχίας, των τριών πλακών. Ιδιο βάρος: go=0.16mx25.0kN/m3= 4.00 kN/m2 Επικάλυψη: ge= 1.00 kN/m2 Σύνολο μόνιμων φορτίων: g= 5.00 kN/m2 Σύνολο ωφέλιμων φορτίων: q= 5.00 kN/m2 Το μόνιμο φορτίο σχεδιασμού κάθε πλάκας ισούται με gd=1.00x5.0=5.0 kN/m και το συνολικό φορτίο σχεδιασμού με pd=γgxg+γ qxq=1.35x5.0+1.50x5.0=14.25 kN/m. I=(bxh3)/12=(1.0x0.163)/12=341x10-6 m4 Το μέτρο ελαστικότητας για σκυρόδεμα C50/60 ισούται με E=37.3 GPa. ExI=37.3x109N/m2x341x10-6m4=12.719x106 Nxm2 Επειδή I10=I12=I23=Ic, οι συντελεστές δυσκαμψίας k και οι δείκτες κατανομής υ ισούνται με:
Λόγω συμμετρίας φορέα : u21=0.571 and u23=0.429 Φόρτιση 1 : w1=w3=pd=14.25 kN/m, w2=gd=5.0 kN/m (V01,max, M01,max, M12,min, |V32,max|, M23,max)
Θεμελιώδεις ροπές πάκτωσης από τον πίνακα b3 → Μ10=Μ23=-w1xL2/8=-14.25x5.02/8=-44.5 kNm, Μ12=Μ21=-w 2xL2/12=-5.0x5.02/12=-10.4 kNm | | | | | | -[+44.5-10.4]x0.429→ -14.6 | | | | +18.8 ← 0.429x[-(+10.4-44.5-9.8)] | | | | | | | | | | |
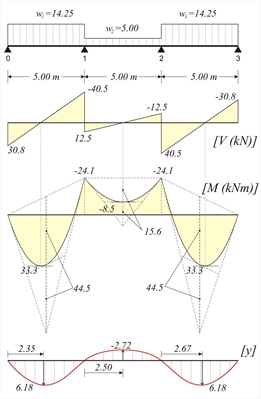 Εικόνα 4.5.3.1-6
Εικόνα 4.5.3.1-6 Εικόνα 4.5.3.1-6 V01=14.25x5.0/2-24.1/5.0=35.63-4.82=30.8 kN M01,max=V012/(2xw1)=30.82/(2x14.25)=33.3 kNm w1xL2/8=14.25x5.02/8=44.5 kNm M12,min=V122/(2xw2)+M1=12.52/(2x5.0)-24.1=15.6-24.1= w2xL2/8=5.0x5.02/8=15.6 kNm C1=(-14.25x5.03/24+30.8x5.02/6)=54.1 kNxm2 (4)→(14.25/6)z3-(30.8/2)z2-0+54.1=0 → 2.375z3-15.4z2+54.1=0 που δίνει λύση zmax=2.347 m (2)→ y(z)=1/12.719x[(14.25/24)x2.3474-(30.8/6)x2.3473+0x2.3472+54.1x2.347)]→ y(2.335)=6.18 mm 12: Λόγω συμμετρίας φορέα και φόρτισης, είναι
zmax=2.5 0m C1=(-5.00x5.03/24+12.5x5.02/6-24.1x5.0/2)kNxm2= =-34.2 kNxm 2 (2) → y(z)=1/12.719x[(5.00/24)x2.504-(12.5/6) x2.503+24.1x2.502/2-34.2x2.50) → y(2.50)=-2.72 mm
Φόρτιση 2 : w1=w3=gd=5.0 kN/m, w2=pd=14.25 kN/m (V01,min, M01,min, M23,max, |V32,min|, M23,min) Θεμελιώδης ροπές πάκτωσης απο τον πίνακα b3 → Μ10=Μ23=-w1xL2/8=-5x5.02/8=-15.6 kNm, Μ12=Μ21=-w2 xL2/12=-14.25x5.02/12=-29.7 kNm | | | | | | -[+15.6-29.7]x0.429 → +6.1 | | | | -7.8 ←0.429x[-(+29.7-15.6+4.0)] | | | | | | | | | | |
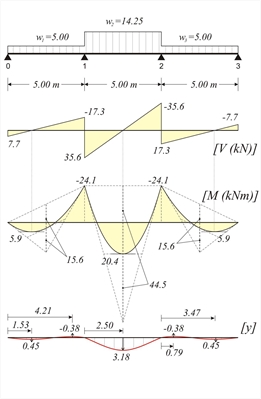 Εικόνα 4.5.3.1-7
Εικόνα 4.5.3.1-7 Εικόνα 4.5.3.1-7 V01=5.0x5.0/2-24.1/5.0=12.5-4.8=7.7 kN M01,max=V012/(2xw1)=7.72/(2x5.0)=5.9 kNm w1xL2/8=5x5.02/8=15.6 kNm M12,max=V122/(2xw2)+M1=35.62 /(2x14.25)-24.1=44.5-24.1=20.4 kNm w2xL2/8=14.25x5.02/8=44.5 kNm C1=(-5.00x5.03/24+7.7x5.02/6)kN x m2=6.0 kNxm2 (4) → (5.00/6)z3-(7.7/2)z2-0+6.0=0 → 0.833z3-3.85z2+6.0=0 gives zmax,1=1.53 m και zmax,2=4.21 m (2) → y(z1)=1/12.719x [(5.00/24) x1.534-(7.7/6) x1.533+0x1.532+6.0x1.53) → y(1.53)=0.45 mm (2) → y(z2)=1/12.719x [(5.00/24) x4.214-(7.7/6) x4.213+0x4.212+6.0x4.21) → y(4.21)=-0.39 mm 12: Λόγω συμμετρίας φορέα και φόρτισης
zmax=2.50 m C1=(-14.25x5.03/24+35.6x5.02/6-24.1x5.0/2)kNxm2= =13.9 kNxm 2 (2) → y(z)=1/12.719x[(14.25/24)x2.504-(35.6/6) x2.503+24.1x2.502/2+13.9x2.50) → y(2.50)=3.18 mm
Φόρτιση 3 : w1=w2=pd=14.25 kN/m, w3=gd =5.0 kN/m (V12,max, |V10,max|, M1,min) Μ10=-w1xL2/8=-14.25x5.02/8=-44.5 kNm, Μ12=-w2xL 2/12=-14.25x5.02/12=-29.7 kNm M23=-w3xL2/8=-5.0x5.02/8=-15.6 kNm | | | | | | -[+44.5-29.7]x0.429 → -6.4 | | | | -4.3← 0.429x[-(+29.7-15.6-4.2)] | | | | | | | | | | |
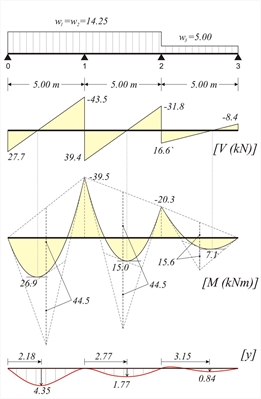 Εικόνα 4.5.3.1-8
Εικόνα 4.5.3.1-8 Εικόνα 4.5.3.1-8 V01=14.25x5.0/2-39.5/5.0=35.6-7.9=27.7 kN V12=14.25x5.0/2+(39.5-20.3)/5.0=39.4 kN V23=5.0x5.0/2+20.3/5.0=12.5+4.1=16.6 kN w1xL2/8=14.25x5.02/8=44.5 kNm w3xL2/8=5.0x5.02/8=15.6 kNm C1=(-14.25x5.03/24+27.7x5.02/6)=41.2 kNxm2 (4) → (14.25/6)z3-(27.7/2)z2-0+41.2=0 → 2.375z3-13.85z2+41.2=0 που δίνει λύση zmax=2.18 m (2) → y(z)=1/12.719x [(14.25/24) x2.184-(27.7/6) x2.183+0x2.182+41.2x2.18) → y(1.53)=4.35 mm 12: C1=(-14.25x5.03/24+39.4x5.02/6-39.5x5.0/2)kNxm2= (4) → (14.25/6)z3-(39.4/2)z2+39.5z-8.8=0 → 2.375z3-19.70z2+39.5z-8.8=0 που δίνει λύση zmax=2.77 m (2)→ y(z)=1/12.719x[(14.25/24)x2.774-(39.4/6)x 2.773+39.5x2.772/2-8.8x2.77)→ y(2.50)=1.77 mm 23:C1=(-5.00x5.03/24+16.6x5.02/6-0.3x5.0/2)kNxm2= (4) → (5.00/6) z3-(16.6/2) z2+20. 3xz-7.6=0 → 03833z3-8.3z2+20.3z-7.6=0 που δίνει 2 λύσεις, μία θετική στο zmax,2=3.15 m και μια αρνητική. (2)→ y(z2)=1/12.719x [(5.00/24) x3.154-(16.6/6) x 3.153+20.3x3.152/2-7.6x3.15)→ y(2.50)=0.84 mm
Φόρτιση 4 : w1=gd=5.0 kN/m w2=w3=pd=14.25 kN/m Η φόρτιση αυτή είναι η αντισυμμετρική ως προς το μέσο της φόρτισης 3. Περιβάλλουσες όλων των φορτίσεων: .jpg?bhow=0&w=500&h=500&Str=0) Εικόνα 4.5.3.1-9: Περιβάλλουσες τεμνουσών-ροπών-βελών κάμψης
Εικόνα 4.5.3.1-9: Περιβάλλουσες τεμνουσών-ροπών-βελών κάμψης Εικόνα 4.5.3.1-9: Περιβάλλουσες τεμνουσών-ροπών-βελών κάμψης m1=10.695, mB=-9.025, m2=17.425, p1A=2.315, p1B=-1.635, p2B=1.805 V01,max=pdxL/p1A=14.25x5.0/2.315=30.8 kN V10,min=pdxL/p1B=-14.25x5.0/1.635=-43.6 kN V12,max=pdxL/p2B=14.25x5.0/1.805=39.5 kN M01,max=pdxL2/m1=14.25x5.02/10.695=33.3 kNm M1,min=pdxL2/mB=-14.25x5.02/9.025=-39.5 kNm M12,max=pdxL2/m2=14.25x5.02/17.425=20.4 kNm Η επίλυση με τον πίνακα είναι πολύ εύκολη, το πρόβλημα όμως είναι ότι δεν δίνει την αρνητική τιμή της ροπής του μεσαίου ανοίγματος.
Επίλυση με το λογισμικό (μελέτη <B_453-1>) Επιλέγοντας την ένδειξη “Δυσμένεια\Πλάκες” από την καρτέλα “Φορτία” του pi-FES, το λογισμικό εξάγει άμεσα τις περιβάλλουσες τεμνουσών δυνάμεων, ροπών κάμψης και βελών κάμψης. Με την επιπλέον επιλογή “Ενεργό module\SLABS” από την καρτέλα “Modules ”, οι τρεις αυτές περιβάλλουσες απεικονίζονται ως εξής: 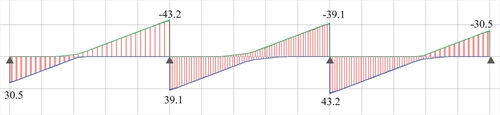 Figure 4.5.3.1-10: Shear force envelope for q=5.0 kN/m2 (Active module\SLABS & Adverse\Slabs)
Figure 4.5.3.1-10: Shear force envelope for q=5.0 kN/m2 (Active module\SLABS & Adverse\Slabs) Figure 4.5.3.1-10: Shear force envelope for q=5.0 kN/m2 (Active module\SLABS & Adverse\Slabs)
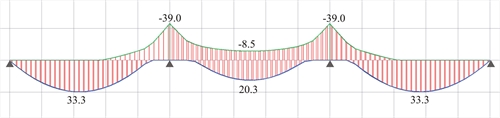 Figure 4.5.3.1-11: Bending moment envelope for q=5.0 kN/m2 (Active module\SLABS & Adverse\Slabs)
Figure 4.5.3.1-11: Bending moment envelope for q=5.0 kN/m2 (Active module\SLABS & Adverse\Slabs) Figure 4.5.3.1-11: Bending moment envelope for q=5.0 kN/m2 (Active module\SLABS & Adverse\Slabs)
 Figure 4.5.3.1-12: Deflection envelope for q=5.0 kN/m2 (Active module\SLABS & Adverse\Slabs)
Figure 4.5.3.1-12: Deflection envelope for q=5.0 kN/m2 (Active module\SLABS & Adverse\Slabs) Figure 4.5.3.1-12: Deflection envelope for q=5.0 kN/m2 (Active module\SLABS & Adverse\Slabs)
Η επίλυση των συνεχών πλακών με ενιαία φόρτιση pd=14.25 kN/m μας δίνει: 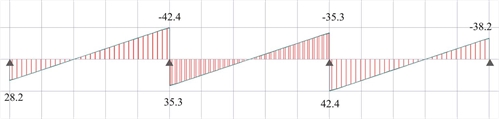 Figure 4.5.3.1-13: Shear force diagram for p=14.25 kN/m (Active module\SLABS)
Figure 4.5.3.1-13: Shear force diagram for p=14.25 kN/m (Active module\SLABS) Figure 4.5.3.1-13: Shear force diagram for p=14.25 kN/m (Active module\SLABS)
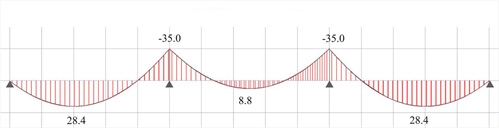 Figure 4.5.3.1-14: Bending moment diagram for p=14.25 kN/m (Active module\SLABS)
Figure 4.5.3.1-14: Bending moment diagram for p=14.25 kN/m (Active module\SLABS) Figure 4.5.3.1-14: Bending moment diagram for p=14.25 kN/m (Active module\SLABS)
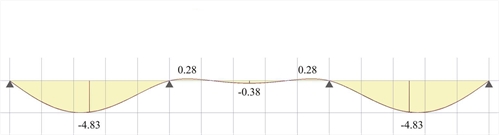 Figure 4.5.3.1-15: Deflection envelope for pd=14.25 kN/m (Active module\SLABS)
Figure 4.5.3.1-15: Deflection envelope for pd=14.25 kN/m (Active module\SLABS) Figure 4.5.3.1-15: Deflection envelope for pd=14.25 kN/m (Active module\SLABS)
Συγκρίνοντας τα αποτελέσματα της ανάλυσης με καθολική φόρτιση και με δυσμενείς φορτίσεις, παρατηρούμε σχετικά μικρές διαφορές όσον αφορά τις τέμνουσες δυνάμεις, ενώ στις ροπές κάμψης των ανοιγμάτων και στα βέλη κάμψης οι διαφορές είναι έντονες κυρίως στο μεσαίο άνοιγμα. Για ωφέλιμο φορτίο ίσο με το σύνηθες κατοικιών (q=2.0 kN/m2) (μελέτη <B_453-2>): pd=γgxg+γqxq=1.35x5.0+1.50x2.0=9.75 kN/m (συνολικό φορτίο σχεδιασμού). Οι αντίστοιχες περιβάλλουσες απεικονίζονται ως εξής:
Παρατηρούμε ότι στην περίπτωση ωφέλιμου φορτίου q=2.0 kN/m2 οι διαφορές των οριακών τιμών είναι μικρότερες από την περίπτωση ωφέλιμου φορτίου q=5.0 kN/m2, αλλά στις ροπές και στα βέλη οι διαφορές παραμένουν σημαντικές. Η εργασία μέσω του πίνακα b4 είναι πολύ εύκολη, προϋποθέτει όμως ίσα ανοίγματα, ίσα πάχη πλακών και ίσα φορτία. Επιπλέον δεν υποστηρίζει πιθανές αρνητικές ροπές ανοιγμάτων, ούτε πιθανές θετικές ροπές στηρίξεων.
Απλοποιημένη μέθοδος εκτίμησης περιβάλλουσας Σε συνήθεις κατασκευές, οι δυσμενείς φορτίσεις μπορεί να παραλείπονται στις στατικές επιλύ-σεις πλακών, αρκεί οι ροπές στηρίξεων και ανοιγμάτων να πολλαπλασιάζονται με ένα συντελεστή προσαύξησης σύμφωνα με τα ακόλουθα.
| |
| | |
| | |
| | |  Figure 4.5.3.2
Figure 4.5.3.2 Figure 4.5.3.2 |
- Σε περίπτωση τετραέρειστων πλακών με περίπου ίσα ανοίγματα, ισχύουν ανάλογες προσαυξήσεις, μικρότερες όμως κατά 50%.
- Στις τέμνουσες δυνάμεις, η μέση προσαύξηση για όλες τις στηρίξεις είναι της τάξης του 10%.
|