Κέντρο ελαστικής στροφής και ελαστικές μετακινήσεις διαφράγματος Στη συγκεκριμένη παράγραφο εξετάζεται η περίπτωση ορθογωνικών κολονών σε παράλληλη διάταξη. Το Παράρτημα Γ αναλύει τη γενική περίπτωση.. .jpg?bhow=0&w=500&h=500&Str=0 "Εικόνα 5.4.3.1-1: Απλό παράδειγμα ορόφου με 4 υποστυλώματα,τα οποία καταλήγουν σε άκαμπτη πλάκα-διάφραγμα.")
Εικόνα 5.4.3.1-1: Απλό παράδειγμα ορόφου με 4 υποστυλώματα,τα οποία καταλήγουν σε άκαμπτη πλάκα-διάφραγμα. Εικόνα 5.4.3.1-1: Απλό παράδειγμα ορόφου με 4 υποστυλώματα,τα οποία καταλήγουν σε άκαμπτη πλάκα-διάφραγμα. .jpg?bhow=0&w=500&h=500&Str=0 "Εικόνα 5.4.3.1-2: Παράλληλη μετατόπιση του διαφράγματος προς τις δύο διευθύνσεις και στροφή,λόγω της δύναμης Η που ασκείται στο κέντρο μάζας C<sub>M</sub>(Χ0Υ αρχικό σύστημα συντεταγμένων, xCTy κύριο σύστημα συντεταγμένων)")
Εικόνα 5.4.3.1-2: Παράλληλη μετατόπιση του διαφράγματος προς τις δύο διευθύνσεις και στροφή,λόγω της δύναμης Η που ασκείται στο κέντρο μάζας CM(Χ0Υ αρχικό σύστημα συντεταγμένων, xCTy κύριο σύστημα συντεταγμένων) Εικόνα 5.4.3.1-2: Παράλληλη μετατόπιση του διαφράγματος προς τις δύο διευθύνσεις και στροφή,λόγω της δύναμης Η που ασκείται στο κέντρο μάζας CM(Χ0Υ αρχικό σύστημα συντεταγμένων, xCTy κύριο σύστημα συντεταγμένων) Η διαφραγματική λειτουργία εξετάζεται ως επαλληλία τριών καταστάσεων: (α) παράλληλη μετατόπιση του διαφράγματος κατά X λόγω οριζόντιας συνιστώσας δύναμης HX, (β) παράλληλη μετατόπιση του διαφράγματος κατά Y λόγω οριζόντιας συνιστώσας δύναμης HY, (γ) στροφή του διαφράγματος λόγω ροπής MCT που ασκείται στον πόλο περιστροφής CT. Οι οριζόντιες σεισμικές δυνάμεις ασκούνται σε κάθε σημείο με μάζα, ενώ η συνισταμένη δύναμη στο κέντρο μάζας CM. Στην περίπτωση που η κατεύθυνση της δύναμης H διέρχεται από το σημείο CT ,η ροπή είναι μηδενική και επομένως το διάφραγμα δεν έχει στροφή. Μετατόπιση του πόλου περιστροφής CT κατά τη διεύθυνση x κατά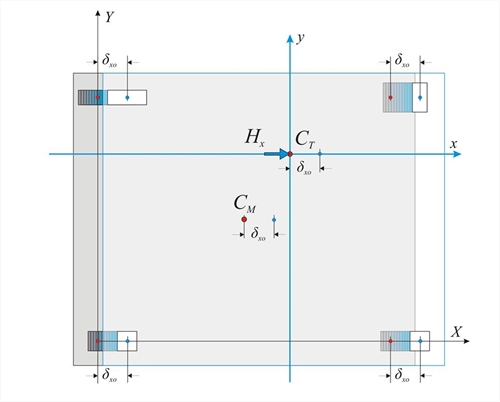 
Εικόνα 5.4.3.2: Παράλληλη μετατόπιση κατά xλόγω της δύναμης Hx που διέρχεται από το CT Εικόνα 5.4.3.2: Παράλληλη μετατόπιση κατά xλόγω της δύναμης Hx που διέρχεται από το CT Στην περίπτωση κατά την οποία ασκείται οριζόντια δύναμη Hx επί του CT κατα x ισχύουν οι 2 ακόλουθες εξισώσεις ισορροπίας: - Το άθροισμα των δυνάμεων κατά τη διεύθυνση x ισούται με Hx, δηλαδή Hx=Σ(Vxoi ) (i).
- • Το άθροισμα των ροπών των Vxoi ως προς το σημείο CT ισούται με μηδέν, δηλαδή Σ(Vxoi ·yi)=0 (ii).
Κάθε κολόνα i αναλαμβάνει τέμνουσα δύναμη Vxoi=δxo· Kxi. Με βάση τη σχέση Σ (Vxoi)= Σ ( δ xo · Kxi)= δ xo · Σ (Kxi), η (i) δίνει Hx=δxo·Σ(Kxi) → Hx=Kx · δ xo where Kx= Σ (Kxi). Η (ii) δίνει Σ(Vxoi·[Yi-YCT])=0 → Σ(Vxoi·Yi )-Σ(Vxoi·YCT)=0 → YCT·Σ(Vxoi)= Σ(Vxoi ·YCT) → YCT= Σ ( δ xo · Kxi · Yi)/ Σ ( δ xo · Kxi) → YCT= Σ (Kxi · Yi)/ Σ (Kxi) Μετατόπιση του πόλου περιστροφής CT κατά τη διεύθυνση y κατά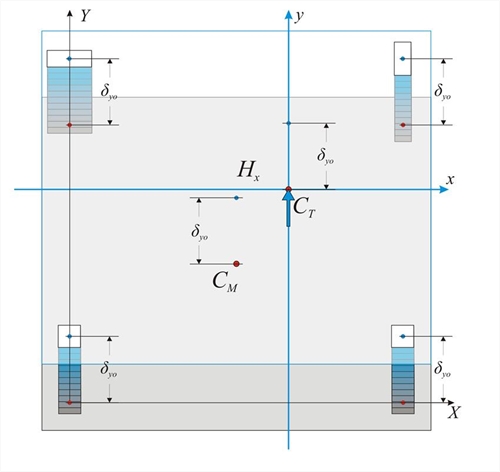 
Εικόνα 5.4.3.3: Παράλληλη μετατόπιση κατά y λόγω της δύναμης Hy Εικόνα 5.4.3.3: Παράλληλη μετατόπιση κατά y λόγω της δύναμης Hy Οι αντίστοιχοι τύποι για τη διεύθυνση y προκύπτουν με όμοιο τρόπο.. Hy=Ky · δ yo όπου Ky=Σ(Kyi) andXCT=Σ(Kyi·Xi)/Σ (Kyi) Συνοψίζοντας, οι σχέσεις που δίνουν το κέντρο ελαστικής στροφής και τις μεταφορικές δυσκαμψίες είναι οι παρακάτω: Κέντρο Ελαστικής Στροφής και Μεταφορικές Δυσκαμψίες: Στροφή θz του διαφράγματος περί τον πόλο περιστροφής θzπερί τον πόλο περιστροφής CT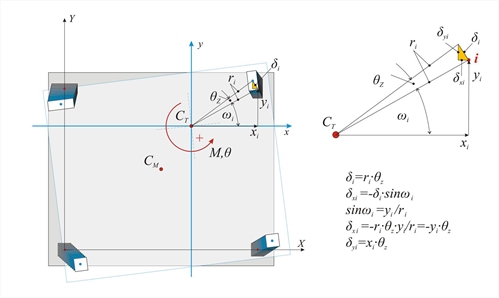 
Εικόνα 5.4.3.4: Μετατοπίσεις λόγω στροφής από ροπή M στο Κέντρο Ελαστικής Στροφής CT Εικόνα 5.4.3.4: Μετατοπίσεις λόγω στροφής από ροπή M στο Κέντρο Ελαστικής Στροφής CT Κύριο σύστημα συντεταγμένων Η παραμόρφωση του διαφράγματος είναι ουσιαστικά μία στροφή θz περί τοCT, η οποία προκαλεί μετατόπιση δi κάθε υποστηλώματος i με συντεταγμένες xi,yi ως προς το σύστημα συντεταγμένων με αρχή το CT. Αν η απόσταση του σημείου i από το CT ισούατι με ri, οι δύο συνιστώσες της (απειροστής) παραμόρφωσης δi ισούνται μεδxi=-θz·yi καιδyi= θz·xi. Οι μετατοπίσεις δ xi, δyi δημιουργούν σε κάθε υποστήλωμα τέμνουσες Vxi και Vyi όπου: Vxi=Kxi · δ xi =Kxi · (- θ z · yi)→ Vxi=-θz·Kxi·yi and Vyi=Kyi·δyi=Kyi·(θz·xi) → Vyi= θz·kyi·xi Η συνισταμένη των ροπών όλων των τεμνουσών Vxi, Vyiως προς το κέντρο ελαστικής στροφής ισούται με την εξωτερική ροπή MCT, δηλαδή MCT= Σ (-Vxi · yi+Vyi · xi+Kzi) → MCT= θ z · Σ (Kxi · yi2+Kyi · xi2+Kzi) Δυστρεψία Kzi υποστηλώματος i Οι κολόνες ανθίστανται στη στροφή του διαφράγματος με την καμπτική τους δυσκαμψία κατά τους όρους Kxi·yi2 , Kyi·xi2 (in N·m), αλλά και με την ίδια τη δυστρεψία τους Kzi, σε μονάδες ροπής N ·m. Η δυστρεψία ενός υποστυλώματος ισούται με Kz=0.5E·Id/h, όπου 0.5Ε είναι το μέτρο διάτμησης Gτου υλικού, το οποίο συνήθως λαμβάνεται ίσο με το 0.5 του μέτρου ελαστικότητας του υλικού της κολόνας, h είναι το ύψος της κολόνας και Id είναι η στρεπτική ροπή αδράνειας της διατομής, το οποίο λαμβάνεται από τον ακόλουθο πίνακα..
| | | |
| | |
| |
| όπου n όπου το n λαμβάνεται από τον πιο κάτω τύπο | Η (ίδια) δυστρεψία των κολονών Kz είναι πολύ μικρή και συνήθως παραλείπεται. Δυστρεψία του διαφραγματικού ορόφου Η ποσότητα Κθ ονομάζεται δυστρεψία (στροφική δυσκαμψία) του διαφράγματος και έχει μονάδες N ·m, κατ’ αναλογία με τις ποσότητες Kx=Σ(Kxi), Ky=Σ (Kyi), οι οποίες ονομάζονται μεταφορικές δυσκαμψίες του διαφράγματος κατά τη διεύθυνση x και y αντίστοιχα και έχουν μονάδες N/m . Δυστρεψία K θ διαφράγματος είναι η ροπή που απαιτείται για να προκαλέσει σχετική στροφή του διαφράγματος κατά μία μονάδα. Έλλειψη και Ακτίνες Δυστρεψίας, Ισοδύναμο Σύστημα Ζητείται: ένα ιδεατό απλό Ισοδύναμο στατικό Σύστημα, το οποίο θα εμφανίζει την ίδια σεισμική συμπεριφορά με το πραγματικό στατικό σύστημα. Απάντηση: Τοποθετούμε4 ιδεατές κολόνες E1, E2 and E3, E4 συμμετρικά ως προσ το κεντρο C T και ως προς τους άξονες x and y, δηλαδή και οι 4 ιδεατές κολόνες έχουν την ίδια απόλυτη τιμή της συντεταγμένηςx και της συντεταγμένης y. Οι ιδεατές κολόνες E1, E2, E3, E4 έχουν η καθεμία δυσκαμψία Kx=1/4·Σ(Kxi) και Ky=1/4 ·Σ(Kyi).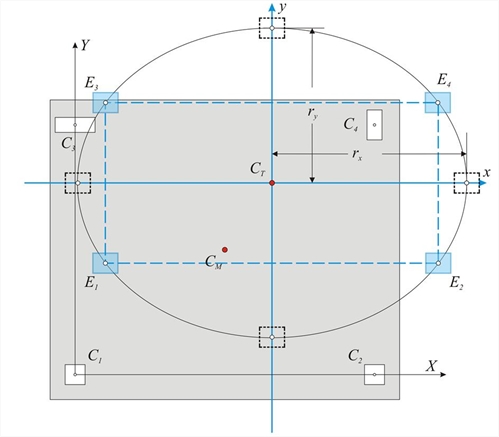 
Εικόνα 5.4.3.5-1 Εικόνα 5.4.3.5-1 Το σύστημα αυτό ικανοποιεί τις 2 συνθήκες του πραγματικού συστήματος, οι οποίες αφορούν τις μετακινήσεις ολίσθησης του διαφράγματος του συνόλου των κολονών. Δυσκαμψία κατα x: 4·1/4·Σ(Kxi)=Σ(Kxi) and stiffness by y: 4·(1/4)·Σ (Kyi)=Σ(Kyi) Για να ικανοποιείται η 3η συνθήκη, το ιδεατό σύστημα θα πρέπει να έχει δυστρεψία K θ, eq =[4 · (1/4) · Σ(Kyi)·y2+4·(1/4)·Σ(Kxi)·x2]=Σ(Kxi)·y2+Σ(Kyi)·x 2 ίση με τη δυστρεψία του πραγματικού συστήματος K θ ,re = Κθ = Σ (Kxi · yi2+Kyi · xi2+Kzi) . Δηλαδή, πρέπει Kθ,eq=Kθ,re → Σ(Kyi)·x2+Σ(Kxi)· y2=Kθ → Ακτίνες δυστρεψίας του διαφράγματος: Η καμπύλη (8’) είναι έλλειψη με κέντρο το CT, διεύθυνση αυτή των κυρίων αξόνων (εν προκειμένω τη διεύθυνση του αρχικού συστήματος) και ημιάξονες rx, ry, (ακτίνες δυστρεψίας του διαφράγματος). Η στρεπτική συμπεριφορά ορόφου περιγράφεται από την ελλειψοειδή γραμμή δυστρεψίας (CT, rx, ry) η οποία παριστάνει την ισοδύναμη κατανομή της δυσκαμψίας του διαφράγματος. Οι ακτίνες rx, ry, της έλλειψης ονομάζονται ακτίνες δυστρεψίας . Υπάρχει απειρία λύσεων ιδεατών διπλών ζευγών συστημάτων, εκ των οποίων το πιο χαρακτηριστικό είναι εκείνο με τις 4 ιδεατές κολόνες στα 4 άκρα της έλλειψης. Γενικά, υπάρχει απειρία λύσεων με n-απλά αντιδιαμετρικά συστήματα, όπου η κάθε ιδεατή κολόνα έχει δυσκαμψίες ίσες με το 1/n των συνολικών δυσκαμψιών του συστήματος. Επαλληλία των τριών καταστάσεων: Όλοι οι προηγούμενοι υπολογισμοί εξαρτώνται από τη γεωμετρία του φορέα και δεν επηρεάζονται από το μέγεθος της εξωτερικής φόρτισης, π.χ. το Κέντρο Ελαστικής Στροφής, οι στατικές εκκεντρότητες ή οι ακτίνες δυστρεψίας είναι ανεξάρτητες από το μέγεθος της σεισμικής δύναμης. Στη συνέχεια, υπολογίζουμε τις παραμορφώσεις και τις εντάσεις του φορέα λόγω της εξωτερικής σεισμικής φόρτισης H. Η εκάστοτε σεισμική δύναμη H ασκείατι στο κέντρο μάζας CM of the diaphragm. Η δύναμη αυτή αναλύεται στις δύο δυνάμεις Hx και Hy παράλληλα με τους δύο άξονες του κύριου συστήματος. Προκειμένου να εφαρμόσουμε την προηγούμενη ανάλυση, μεταφέρουμε τις δυνάμεις Hx, Hy στο κέντρο ελαστικής στροφής CTμαζί με τη ροπή MCT βάσει της σχέσης: Ροπή σεισμού στο Κέντρο Ελαστικής Στροφής: Με τα εξωτερικά μεγέθη Hx, Hy, γ MCT υπολογίζουμε: - τις μετακινήσεις δ xo , δ yo and θ z του πόλου περιστροφής του διαφράγματος
Μετακινήσεις του Κέντρου Ελαστικής Στροφής: - τις μετακινήσεις δ xi , δ yi της κεφαλής κάθε κολόνας
- τις τέμνουσες και τις ροπές κάθε υποστυλώματος στο τοπικό του σύστημα
Σεισμικές Τέμνουσες και Σεισμικές Ροπές: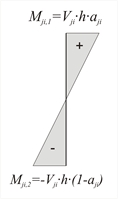 
Εικόνα 5.4.3.5-2 Εικόνα 5.4.3.5-2 - Η κατανομή των τεμνουσών δυνάμεων σε κάθε κολόνα εξαρτάται μόνο από τη γεωμετρία του στατικού συστήματος. Αυτό σημαίνει ότι στην περίπτωση που το μέτρο ελαστικότητας του υλικού των κολονών μεταβληθεί, οι μετατοπίσεις των κολονών θα αλλάξουν, όχι όμως και οι τέμνουσες.
- Όσο περισσότερο απέχει μία κολόνα από το κέντρο ελαστικής στροφής, τόσο μεγαλύτερη είναι η επιρροή της στροφής. Συμπεραίνουμε, λοιπόν, ότι οι κολόνες που βρίσκονται στην περίμετρο του ορόφου εμφανίζουν τη μεγαλύτερη στροφική επιβάρυνση.
- Οι παραμορφώσεις λόγω στροφής εξαναγκάζουν τις κολόνες σε διαξονική κάμψη, δηλαδή σε ταυτόχρονη κάμψη και στις δύο διευθύνσεις τους, γι’ αυτό η στροφή πρέπει να περιορίζεται όσο το δυνατόν περισσότερο.
- Οι παραμορφώσεις λόγω στροφής εξαναγκάζουν τις κολόνες σε διαξονική κάμψη, δηλαδή σε ταυτόχρονη κάμψη και στις δύο διευθύνσεις τους, γι’ αυτό η στροφή πρέπει να περιορίζεται όσο το δυνατόν περισσότερο.
- Ακόμη και σε συμμετρικούς γεωμετρικά φορείς, οι τυχηματικές εκκεντρότητες [*]
 NoteΒλέπε κεφάλαιο 6. δημιουργούν έντονες διαξονικές εντάσεις και γι’ αυτό η ύπαρξη υψηλής δυστρεψίας είναι εξαιρετικά χρήσιμη. Υψηλή δυστρεψία επιτυγχάνεται κυρίως με διάταξη ισχυρών κολονών, συνήθως τοιχίων, στην περίμετρο του κτιρίου. - Η ισχυρή δυστρεψία είναι απαραίτητη όχι μόνο σε αντισεισμικά κτίρια, αλλά και σε κάθε κτίριο, το οποίο ενδέχεται να καταπονηθεί από οριζόντιες δράσεις, όπως ο άνεμος, από ασύμμετρο χιόνι, ή από άλλους απρόβλεπτους παράγοντες.
- Η δυστρεψία ενός διαφραγματικού ορόφου εξαρτάται κυρίως από τη θέση του κέντρου ελαστικής στροφής σε σχέση με το κέντρο μάζας και από το μέγεθος των ακτίνων δυστρεψίας.Οι δύο αυτοί παράγοντες εξαρτώνται μόνο από τη γεωμετρία του φορέα και όχι από το μέγεθος των σεισμικών φορτίσεων.
|