ΔΥΣΚΑΜΨΙΑ ΕΠΙΠΕΔΩΝ ΠΟΛΥΩΡΟΦΩΝ ΠΛΑΙΣΙΩΝ Β.1 Δυσκαμψία ζυγώματος πλαισίου Η αξιολόγηση της λειτουργίας μονώροφου επίπεδου πλαισίου σε οριζόντιες σεισμικές δυνάμεις, αναπτύχθηκε στην §5.1. Εκεί εξηγήθηκε η λειτουργία κάθε υποστυλώματος του πλαισίου και το βασικό μέγεθος που μετρούσε τη στατική λειτουργία της κολόνας ήταν η δυσκαμψία της. Αυτό που ενδιέφερε κυρίως ήταν η σχέση των δυσκαμψιών των κολονών μεταξύ τους. Στα πολυώροφα επίπεδα πλαίσια, το μέγεθος μέτρησης της λειτουργίας σε οριζόντιες σεισμικές δυνάμεις είναι η δυσκαμψία του κάθε ζυγώματος. Ζύγωμα είναι το οριζόντιο τμήμα του πλαισίου που συνδέει τις κολόνες μεταξύ τους. Το ζύγωμα συνήθως είναι πλακοδοκός, αλλά μπορεί να είναι και ζώνη πλάκας. Αν τα ζυγώματα 4 και 5 στο φορέα του παρακάτω πλαισίου συνδέονταν μεταξύ τους με πλάκα, τότε θα αποτελούσαν μόνο ένα ζύγωμα (δηλαδή εδώ η έννοια του ζυγώματος θα αντιστοιχούσε στην έννοια του διαφράγματος). 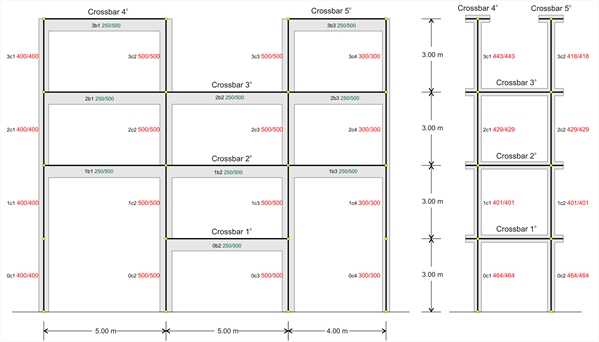 Εικόνα B.1-1: Πλαίσιο της πράξης και ισοδύναμο Σύστημα
Εικόνα B.1-1: Πλαίσιο της πράξης και ισοδύναμο Σύστημα Εικόνα B.1-1: Πλαίσιο της πράξης και ισοδύναμο Σύστημα Δυσκαμψία Ki , ζυγώματος i, επίπεδου πλαισίου είναι ο λόγος της οριζόντιας σεισμικής δύναμης H που εξασκείται επί του ζυγώματος, παράλληλα προς το επίπεδο του πλαισίου, προς την αντίστοιχη μετακίνησηδi του ζυγώματος, δηλαδή Ki=H/δi. Για να συγκρίνουμε μεταξύ τους τις δυσκαμψίες των ορόφων, είναι πολύ εξυπηρετικό να χρησιμοποιήσουμε έναν απλούστερο πλαισιακό φορέα, ο οποίος θα έχει την ίδια συμπεριφορά με το πραγματικό πλαίσιο, σε οριζόντιες σεισμικές δυνάμεις. Υπολογισμός δυσκαμψίας του ζυγώματος i | | Εικόνα B.1-3: Πλαίσιο της πράξης
Αποτελέσματα της επίλυσης του πλαισίου,
μετακινήσεις στο ζύγωμα δi και τέμνουσες στις κολόνες
(Δυσκαμψία ζυγώματος i: Ki=H/δi) Παράδειγμα μελέτης <B_b1-1>:
για Η=100 kN και i=2, δ2=2.589 mm à
K2=H/δ2=100·103N/(2.589·10-3m)=38.6·106 N/m | Εικόνα B.1-4: Ισοδύναμο Σύστημα
Η επίλυση δίνει τις ίδιες μετακινήσεις στο ζύγωμα i, άρα και την ίδια
δυσκαμψία του ζυγώματος i Παράδειγμα μελέτης < B_b1-2>: για Η=100 kN, δ2=2.589 mm àK2=38.6·106 N/m | Παρατηρήσεις:  Εικόνα B.1-5
Εικόνα B.1-5 Εικόνα B.1-5 - Οι μετακινήσεις των κόμβων ενός ζυγώματος γενικά, διαφέρουν κατά τι μεταξύ τους, λόγω αξονικών δυνάμεων. Συνήθως όμως στα ζυγώματα υπάρχουν πλάκες που δημιουργούν όχι μόνο ισχυρές πλακοδοκούς, αλλά και οριζόντια διαφράγματα τα οποία θεωρούνται απαραμόρφωτα αξονικά.
- Σημαντικές μετακινήσεις υπάρχουν σε όλους τους κόμβους των ορόφων, όπως υπάρχουν και τέμνουσες σε όλες τις κολόνες και δοκούς, οι τέμνουσες όμως των ράβδων των ζυγωμάτων πάνω από το ζύγωμα i, είναι πολύ μικρές.
- Οι παραδοχές των δυσκαμψιών με τις οποίες έχουν γίνει οι επιλύσεις του κανονικού και του ιδεατού πλαισίου:
Β.2 Ισοδύναμο πολυώροφο πλαίσιο - σχετική δυσκαμψία ζυγώματος Το ισοδύναμο πλαίσιο μπορεί να αποτελείται από μία, δύο ή περισσότερες κατακόρυφες κολόνες και πρέπει να δίνει τις ίδιες μετακινήσεις με το πραγματικό πλαίσιο. Είναι πιο παραστατικό να χρησιμοποιείται δίστυλο πλαίσιο με ισοδύναμες αμφίπακτες κολόνες και να τοποθετούνται επί αυτού πιθανά διακοπτόμενα ζυγώματα. Η δυσκαμψία των ιδεατών κολονών κάθε ζυγώματος αφορούν τον κάθε όροφο ξεχωριστά και πρέπει το άθροισμά τους να ισούται με το άθροισμα των δυσκαμψιών του πραγματικού ζυγώματος του συγκεκριμένου ορόφου. Για να είναι εφικτό αυτό ορίζουμε τη σχετική δυσκαμψία ζυγώματος ορόφου. Το ιδεατό σύστημα του παραδείγματος αυτής της παραγράφου έχει ένα ζύγωμα σε καθέναν από τους τρεις πρώτους ορόφους και δύο ξεχωριστές αμφίπακτες κολόνες στον τέταρτο όροφο. Το άθροισμα των δυσκαμψιών των δύο ιδεατών κολονών στις τρεις πρώτες στάθμες ισούται με το άθροισμα των δυσκαμψιών των τεσσάρων κολονών του πραγματικού πλαισίου. Στην τέταρτη στάθμη η αριστερή ιδεατή κολόνα αντιστοιχεί στο αριστερό ζύγωμα με τις δύο κολόνες του πραγματικού πλαισίου και η δεξιά ιδεατή κολόνα στο δεξιό ζύγωμα με τις δύο κολόνες του πραγματικού πλαισίου. Σχετική δυσκαμψία KRi , ζυγώματος i, επίπεδου πολυώροφου πλαισίουείναι ο λόγος της οριζόντιας σεισμικής δύναμης Η που εξασκείται επί του ζυγώματος του ορόφου, προς την αντίστοιχη μετακίνηση του ζυγώματος δi σε σχέση με την αντίστοιχη μετακίνηση δi-1 του υποκείμενου ζυγώματοςi-1, όταν επί αυτού εξασκηθεί η ίδια οριζόντια δύναμη Η, δηλαδή KRi=H/(δi -δi-1). Υπολογισμός σχετικής δυσκαμψίας του ζυγώματος i
Παράδειγμα μελέτης < B_b1-1> | 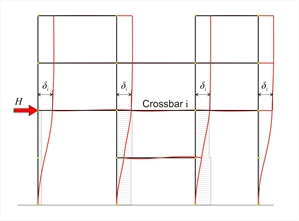 Εικόνα B.2-1: Επίλυση του ζυγώματος i με οριζόντια δύναμη H
Εικόνα B.2-1: Επίλυση του ζυγώματος i με οριζόντια δύναμη H Εικόνα B.2-1: Επίλυση του ζυγώματος i με οριζόντια δύναμη H | 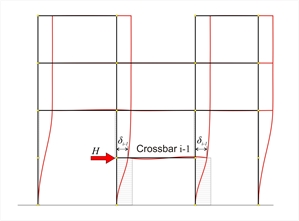 Εικόνα B.2-2: Επίλυση του ζυγώματος i-1 με οριζόντια δύναμη H
Εικόνα B.2-2: Επίλυση του ζυγώματος i-1 με οριζόντια δύναμη H Εικόνα B.2-2: Επίλυση του ζυγώματος i-1 με οριζόντια δύναμη H | Εικόνα B.2-1: Επίλυση του ζυγώματος i
με οριζόντια δύναμη H Παράδειγμα: για Η =100 kN και
i=2, δ 2 =2.589 mm | Εικόνα B.2-2: Επίλυση του ζυγώματος i-1
με οριζόντια δύναμη H Παράδειγμα: για Η =100 kN και
i-1=1, δ 1 =0.936mm | Παράδειγμα: ΚΖ ,2 =100.00 ·103N/[(2.589-0.936)·10-3m=60.5 N/m | | |
Παρατήρηση : Στην ειδική περίπτωση i=1, KΖ,1=K1=100.00·103N/(0.936·10-3m)=106.8 N/m, δηλαδή στην πρώτη στάθμη, σχετική και απόλυτη δυσκαμψία συμπίπτουν. Οι δυσκαμψίες που προκύπτουν από την εφαρμογή των παραπάνω ορισμών, εξαρτώνται μόνο από τη γεωμετρία του πλαισίου και όχι από το μέγεθος της φόρτισης, δηλαδή αν εξασκήσουμε διπλάσια φόρτιση, θα λάβουμε διπλάσιες μετακινήσεις και η δυσκαμψία θα έχει πάλι την ίδια τιμή. Αν βάλουμε όλη την παραπάνω λογική σε ένα πίνακα, θα έχουμε για το σύνολο των ζυγωμάτων τις δυσκαμψίες Κi και τις σχετικές δυσκαμψίες ΚZi | Ζύγωμα i | δo,i | Κi | δi-δi-1 | ΚZi | Ισοδύναμες
διατομές | | | Mm | ·106 N/m | mm | ·106 N/m | mm/mm | | 5 | 6.6789 | 14.97 | 2.810(*) | 35.59 | 418/418 | | 4 | 6.1173 | 16.35 | 2.248 | 44.48 | 443/443 | | 3 | 3.869 | 25.85 | 1.280 | 78.13 | 429/429 | | 2 | 2.589 | 38.62 | 1.653 | 60.50 | 401/401 | | 1 | 0.936 | 106.84 | 0.936 | 106.84 | 464/464 | (*) Εδώ το υποκείμενο ζύγωμα είναι το 3 και όχι το 4 Β.3 Σχετική Δυσκαμψία κολόνας ζυγώματος Για λόγους πληρότητας και σύγκρισης με τα μονώροφα πλαίσια της §5.1, ορίζουμε και τη σχετική δυσκαμψία κολόνας ορόφου. Σχετική δυσκαμψία κολόνας ζυγώματος επίπεδου πλαισίου είναι ο λόγος της τέμνουσας της κολόνας του ζυγώματος προς τη δύναμη H επί τη σχετική δυσκαμψία KRi του ζυγώματος. Οι τέμνουσες Vi,j που αναλαμβάνει η κολόνα j της στάθμης i και
οι αντίστοιχες σχετικές δυσκαμψίες ΚZi,j | Ζύγωμα | ΚZ | Vi,1 | ΚZi,1 | Vi,2 | ΚZi,2 | Vi,3 | ΚZi,3 | Vi,4 | ΚZi,4 | Σ(Vi) | | | ·106 N/m | kN | ·106N/m | kN | ·106N/m | kN | ·106N/m | kN | ·106N/m | | | 5 | 35.59 | - | - | - | - | 75.8 | 27.0 | 24.2 | 8.6 | 100.00 | | 4 | 44.48 | 38.8 | 17.3 | 61.2 | 27.2 | - | - | - | - | 100.00 | | 3 | 78.13 | 18.6 | 14.5 | 36.6 | 28.6 | 34.9 | 27,3 | 9.9 | 7.7 | 100.00 | | 2 | 60.50 | 9.0 | 5.4 | 44.2 | 26.7 | 43.6 | 26.4 | 3.2 | 1.9 | 100.00 | | 1 | 106.84 | 4.0 | 4.3 | 47.3 | 50.5 | 47.3 | 50.5 | 1.4 | 1.5 | 100.00 | Σημαντικό: Η εξέταση της λειτουργίας των πολυώροφων πλαισίων δεν έχει μόνο εκπαιδευτικό χαρακτήρα, αλλά αποτελεί και τη βάση αξιολόγησης των πολυώροφων χωρικών πλαισίων, τα οποία λειτουργούν προς τις δύο επίπεδες πλαισιακές κατευθύνσεις x και y. Βέβαια, στο χωρικό πλαίσιο υπάρχει και ο παράγοντας της στροφής, ο οποίος εξετάζεται στο παράρτημα Δ. Β.4 Επιρροή πλακών στις δυσκαμψίες με χρήση πεπερασμένων στοιχείων Ως ενδεικτικό παράδειγμα επιλύεται ένα τετραώροφο πλαίσιο με υποστυλώματα ύψους 3.0 m σε κάθε όροφο, διατομής 400/400, δοκών ανοίγματος 6.0 m με διατομή 300/500 και πλάκες γεωμετρικού πλάτους 1.0 m εκατέρωθεν των παρειών δοκών, με πάχος 150 mm. Πραγματοποιούνται δύο επιλύσεις: 1η επίλυση : επιλύεται επίπεδο πλαίσιο, όπου η επιρροή των πλακών λαμβάνεται υπόψη με τη θεώρηση συνεργαζόμενου πλάτους των δοκών κατά EC2. Στην ανάλυση πλαισίων, συνήθως, προσομοιώνονται οι δοκοί και οι κολόνες με γραμμικά μέλη. Η επιρροή των πλακών λαμβάνεται υπόψη προσθέτοντας στην ορθογωνική δοκό ένα πέλμα πλάτους beff. 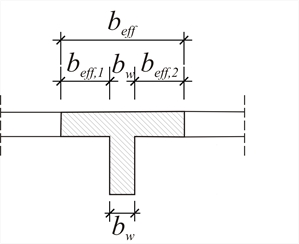 Εικόνα B.4-1
Εικόνα B.4-1 Εικόνα B.4-1
Δημιουργείται δηλαδή μία πλακοδοκός, η οποία συνήθως έχει μορφή T. Το πλάτος b eff ονομάζεται συνεργαζόμενο πλάτος και λαμβάνει κάποιες συμβατικές τιμές. Το μέγεθος του συνεργαζόμενου πλάτους, όπως φαίνεται στην §3.1.2, λαμβάνει υπόψη ορισμένους παράγοντες, όπως το άνοιγμα της δοκού, την απόσταση από τις γειτονικές δοκούς, κτλ. Στο συγκεκριμένο παράδειγμα είναι beff ,1 = beff ,2 =0.50 m à beff =0.50+0.30+ 0.50=1.30 m .
2η επίλυση : επιλύεται επίπεδο πλαίσιο, όπου η επιρροή των πλακών λαμβάνεται υπόψη με τη χρήση επιφανειακών πεπερασμένων στοιχείων. Το μέγεθος των πεπερασμένων στοιχείων έχει ληφθεί 0.30 m γενικά και 0.15 m για την περίμετρο των πλακών. Η μελέτη που χρησιμοποιείται είναι η <B_b4>. στην οποία γίνονται δύο διαφορετικές επιλύσεις, των οποίων οι προκύπτουσες μετακινήσεις παρουσιάζονται παράλληλα στις δύο επόμενες σελίδες, ενώ στην τρίτη σελίδα τα αποτελέσματα και τα συμπεράσματα. Και στις δύο επιλύσεις οι συντελεστές δυσκαμψίας όλων των ράβδων λαμβάνονται ίσοι με 1.0, χρησιμοποιούνται στερεά σώματα, ενώ λαμβάνεται υπόψη και η επιρροή της διάτμησης. Κριτήριο σύγκρισης είναι η δυσκαμψία του ζυγώματος της 3ης στάθμης. Για τις δύο επιλύσεις απαιτείται η ίδια διαδικασία μέχρι ένα σημείο: ‘Παράμετροι’ à ‘Οριζόντιες δυνάμεις’ à ‘Σεισμικές δυνάμεις’. Σε μία στάθμη π.χ. την 3η πληκτρολογούμε στο αντίστοιχο πεδίο την τιμή 100 (όλες οι υπόλοιπες τιμές να είναι μηδενικές) και στη συνέχεια ενεργοποιούμε το ‘Εφαρμογή δυνάμεων’. Τέλος εκτελούμε τον αντισεισμικό υπολογισμό. Για την 1η επίλυση, επιλέγουμε απευθείας ‘Αποτελέσματα ανάλυσης’, όπου ενεργοποιούμε ταυτόχρονα (πατημένο Ctrl) τα ‘Στερεά Κτιρίου’, ‘Χωρικό Μοντέλο’, ‘Παραμορφ. Χωρ.’ και την εμφάνιση τιμών. Για τη 2η επίλυση, τα ‘Αποτελέσματα ανάλυσης’ θα εμφανιστούν, αφού επιλέξουμε επίλυση με πεπερασμένα στοιχεία δηλαδή το πλήκτρο pi-FES. 1η επίλυση: πλαισιακός φορέας υπό οριζόντιο φορτίο H στην 3η στάθμη με προσομοίωση ραβδωτών στοιχείων 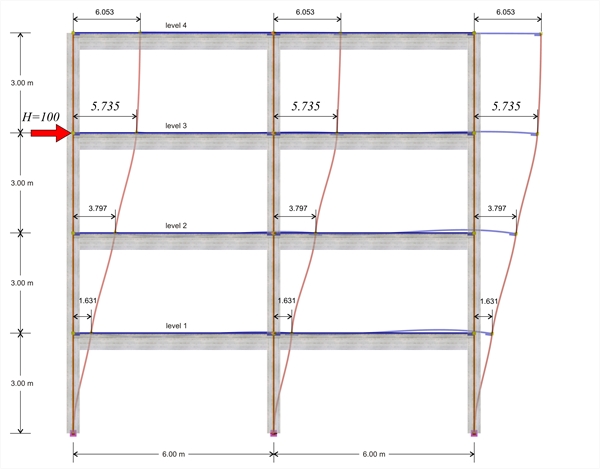 Εικόνα B.4-2: Η παραμόρφωσή του φορέα
Εικόνα B.4-2: Η παραμόρφωσή του φορέα Εικόνα B.4-2: Η παραμόρφωσή του φορέα
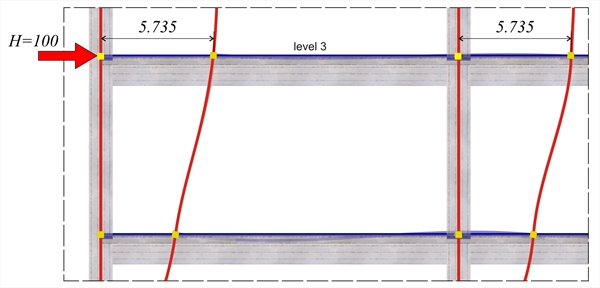 Εικόνα B.4-3: Λεπτομέρεια παραμόρφωσης των μελών της 3ης στάθμης (2ος όροφος)
Εικόνα B.4-3: Λεπτομέρεια παραμόρφωσης των μελών της 3ης στάθμης (2ος όροφος) Εικόνα B.4-3: Λεπτομέρεια παραμόρφωσης των μελών της 3ης στάθμης (2ος όροφος)
2η επίλυση: Πλαισιακός φορέας υπό οριζόντιο φορτίο H στην 3η στάθμη με προσομοίωση ραβδωτών και επιφανειακών πεπερασμένων στοιχείων 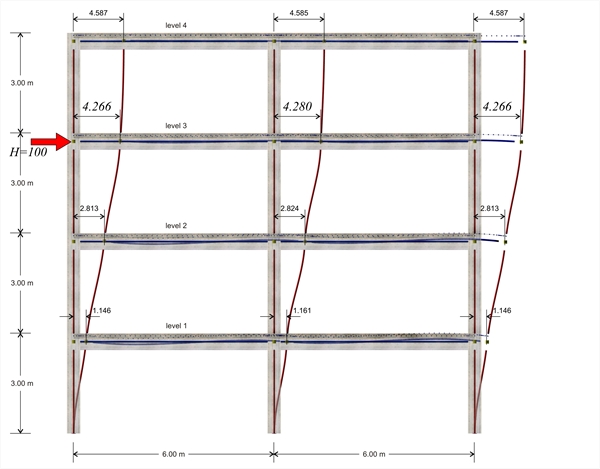 Εικόνα B.4-4: Η παραμόρφωσή του φορέα
Εικόνα B.4-4: Η παραμόρφωσή του φορέα Εικόνα B.4-4: Η παραμόρφωσή του φορέα
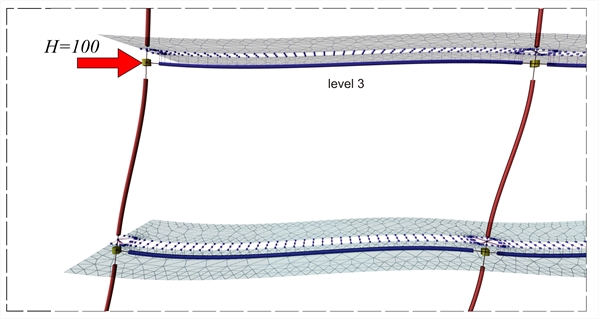 Εικόνα B.4-5: Λεπτομέρεια παραμόρφωσης των μελών και των πεπερασμένων στοιχείων πλάκας της 3ης στάθμης (2ος όροφος)
Εικόνα B.4-5: Λεπτομέρεια παραμόρφωσης των μελών και των πεπερασμένων στοιχείων πλάκας της 3ης στάθμης (2ος όροφος) Εικόνα B.4-5: Λεπτομέρεια παραμόρφωσης των μελών και των πεπερασμένων στοιχείων πλάκας της 3ης στάθμης (2ος όροφος)
Αποτελέσματα 1ης επίλυσης: όπως προκύπτει από τις προηγούμενες σελίδες, για οριζόντια δύναμη H=100 kN, λαμβάνουμε μετακίνηση του ζυγώματος της 3ης στάθμης δ3,1=5.735 mm οπότε η δυσκαμψία του ζυγώματος προκύπτει K3,1=H/δ3,1=100.0·103N/(5.735·10-3m)=17.4·106 N/m. Με ανάλογες αναλύσεις, ασκώντας ξεχωριστά σε κάθε όροφο i τη δύναμη H=100 kN προκύπτουν οι παρακάτω ελαστικές μετακινήσεις δi,1 και οι δυσκαμψίες Ki,1. 4η στάθμη: H=100 kN, δ4,1=8.051 mm, K4,1 =12.4·106 N/m 3η στάθμη: H =100 kN , δ3,1= 5.735 mm , K 3,1 =17.4·106 N / m 2η στάθμη: H=100 kN δ2,1=3.500 mm, K2,1 =28.6·106 N/m 1η στάθμη: H=100 kN, δ1,1=1.358 mm, K1,1 =73.6·106 N/m Αποτελέσματα 2ης επίλυσης: όπως προκύπτει από την προηγούμενη σελίδα, για οριζόντια δύναμη H=100.0 kN, λαμβάνουμε μετακίνηση του ζυγώματος της 3ης στάθμης δ3,2=4.266 mm οπότε η δυσκαμψία του ζυγώματος προκύπτει K3,2=H/δ3,2=100.0·103N/(4.266·10-3m)=23.4·106 N/m. Με ανάλογες αναλύσεις, εξασκώντας ξεχωριστά σε κάθε όροφο i τη δύναμη H=100 kN προκύπτουν οι παρακάτω ελαστικές μετακινήσεις δi,1 και οι δυσκαμψίες Ki,1. 4η στάθμη: H=100 kN, δ4,2=6.073 mm, K4,2 =16.5·106 N/m 3η στάθμη: H =100 kN , δ3,2= 4.266 mm , K 3,2 =23.4·106 N / m 2η στάθμη: H=100 kN δ2,2=2.528 mm, K2,2 =39.6·106 N/m 1η στάθμη: H=100 kN, δ1,2=0.886 mm, K1,2 =112.9·106 N/m Στο συγκεκριμένο παράδειγμα, στην 3η στάθμη, η δυσκαμψία με χρήση πεπερασμένων επιφανειακών στοιχείων προκύπτει μεγαλύτερη κατά (23.4-17.4)/17.4=34% και στην 4η, 2η και 1η στάθμη, αντίστοιχα: 33%, 38% και 53%. Συμπέρασμα : Η δυσκαμψία του πλαισίου προκύπτει μεγαλύτερη όταν η ανάλυση γίνει με τη χρήση επιφανειακών πεπερασμένων στοιχείων.
Β.5 Επιρροή τοιχίων στις δυσκαμψίες με χρήση πεπερασμένων στοιχείων Επειδή η επιρροή των πλακών στη δυσκαμψία εξετάσθηκε στην προηγούμενη παράγραφο, για να προκύψουν αποτελέσματα συγκρίσιμα μεταξύ τους, εξετάζεται στη συνέχεια ένα πλαίσιο με δοκούς χωρίς πλάκες. Ως ενδεικτικό παράδειγμα επιλύεται ένα τετραώροφο πλαίσιο με ίδιες διατομές και ίδιο ύψος 3.0 m σε κάθε όροφο. Κάθε όροφος έχει δύο υποστυλώματα διατομής 400/400 και ένα τοιχίο διατομής 2000/300, ενώ οι δύο δοκοί έχουν άνοιγμα 6.0 m και διατομή 300/500. Τα υποστυλώματα και οι δοκοί προσομοιώνονται με γραμμικά μέλη, ενώ τα τοιχία μπορούν να προσομοιωθούν ή με γραμμικά μέλη που έχουν στερεά σώματα στην κορυφή τους, ή με επιφανειακά πεπερασμένα στοιχεία. Πραγματοποιούνται δύο επιλύσεις: 1η επίλυση : επίπεδο πλαίσιο, όπου τα τοιχία προσομοιώνονται ως γραμμικά μέλη με στερεά σώματα στην κορυφή τους. 2η επίλυση : επίπεδο πλαίσιο, όπου τα τοιχία προσομοιώνονται με τριγωνικά πεπερασμένα στοιχεία. Το μέγεθος των πεπερασμένων στοιχείων έχει ληφθεί 0.30 m γενικά και 0.15 m για την περίμετρο των τοιχίων. Και στις δύο επιλύσεις οι συντελεστές δυσκαμψίας όλων των ράβδων λαμβάνονται ίσοι με 1.0, χρησιμοποιούνται στερεά σώματα, ενώ λαμβάνεται υπόψη και η επιρροή της διάτμησης. Κριτήριο σύγκρισης είναι η δυσκαμψία του ζυγώματος της 3ης στάθμης. Στις επόμενες σελίδες παρουσιάζονται αποτελέσματα και συμπεράσματα από τις δύο επιλύσεις. Μελέτη < B_b5>.
1η επίλυση: Μικτός φορέας υπό οριζόντιο φορτίο H στην 3η στάθμη με προσομοίωση ραβδωτών στοιχείων 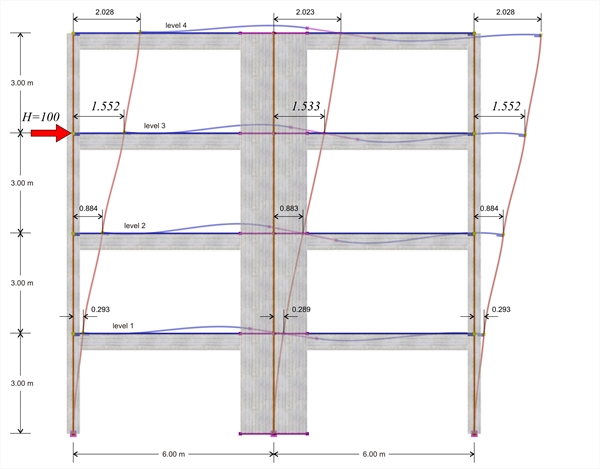 Εικόνα B.5-1: Η παραμόρφωσή του φορέα
Εικόνα B.5-1: Η παραμόρφωσή του φορέα Εικόνα B.5-1: Η παραμόρφωσή του φορέα
Αποτελέσματα 1ης επίλυσης: Για οριζόντια δύναμη H=100 kN, λαμβάνουμε μετακίνηση του ζυγώματος της 3ης στάθμηςδ3,1=1.552 mm οπότε η δυσκαμψία του ζυγώματος προκύπτει K3,1=H/δ3,1=100.0·103N/(1.552·10-3m)=64.4·106 N /m. Με ανάλογες αναλύσεις, εξασκώντας ξεχωριστά σε κάθε όροφο i τη δύναμη H=100 kN προκύπτουν οι παρακάτω ελαστικές μετακινήσεις δi,1 και οι δυσκαμψίες Ki,1. 4η στάθμη: H =100 kN , δ4,1=3.033 mm , K 4,1 =33.0·106 N / m 3η στάθμη: H =100 kN , δ3,1= 1.552 mm , K 3,1 =64.4·106 N / m 2η στάθμη: H =100 kN δ2,1=0.629 mm , K 2,1 =159.0·106 N / m 1η στάθμη: H =100 kN , δ1,1=0.146 mm , K 1,1 =685.0·106 N / m
2η επίλυση: Μικτός φορέας υπό οριζόντιο φορτίο H στην 3η στάθμη με προσομοίωση ραβδωτών και επιφανειακών πεπερασμένων στοιχείων 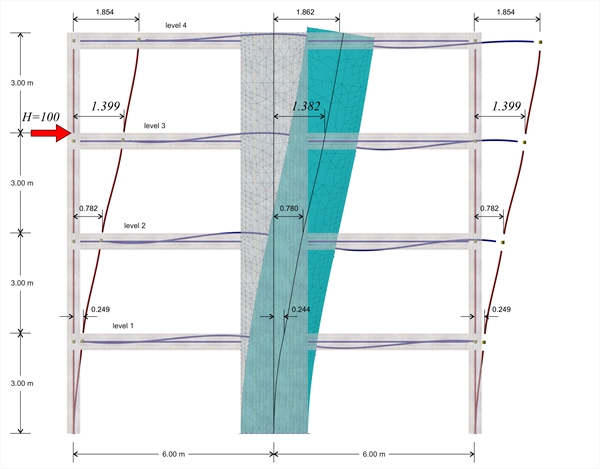 Εικόνα B.5-2: Η παραμόρφωσή του φορέα
Εικόνα B.5-2: Η παραμόρφωσή του φορέα Εικόνα B.5-2: Η παραμόρφωσή του φορέα
Αποτελέσματα 2ης επίλυσης: όπως προκύπτει από την προηγούμενη σελίδα, για οριζόντια δύναμη H=100.0 kN, λαμβάνουμε μετακίνηση του ζυγώματος της 3ης στάθμης δ3,2=1.399 mm οπότε η δυσκαμψία του ζυγώματος προκύπτει K3,1=H/δ3,1=100.0·103N/(1.399·10-3m)=71.5·106 N/m. Με ανάλογες αναλύσεις, εξασκώντας ξεχωριστά σε κάθε όροφο i τη δύναμη H=100 kN προκύπτουν οι παρακάτω ελαστικές μετακινήσεις δi,1 και οι δυσκαμψίες Ki,1. 4η στάθμη: H=100 kN, δ4,2=2.783 mm, K4,2 =35.9·106 N/m This is some text!3η στάθμη: H=100 kN, δ3,2=1.399 mm, K 3,2=71.5·106 N/m 2η στάθμη: H=100 kN δ2,2=0.543 mm, K2,2 =184.0·106 N/m 1η στάθμη: H=100 kN, δ1,2=0.117 mm, K1,2 =855.0·106 N/m Στο συγκεκριμένο παράδειγμα, στη 3η στάθμη, η δυσκαμψία με χρήση πεπερασμένων επιφανειακών στοιχείων προκύπτει μεγαλύτερη κατά (71.5-64.4)/64.4=11% και στην 4η, 2η και 1η στάθμη, αντίστοιχα: 9%, 16% και 25% Συμπέρασμα: Η δυσκαμψία του πλαισίου δε διαφέρει πολύ όταν η ανάλυση στα τοιχία γίνει με τη χρήση επιφανειακών πεπερασμένων στοιχείων. |