Μονώροφο χωρικό πλαίσιο με ορθογωνικές κολόνες Το μονώροφο χωρικό πλαίσιο της εικόνας επιλύεται σε οριζόντια σεισμική δύναμη H=90.6 kN με τέσσερις τρόπους: (i) με το χέρι θεωρώντας άπειρη την κατακόρυφη δυσκαμψία των δοκών, (ii) με το excel και την ίδια θεώρηση, (iii) με το excel και θεώρηση μέσου συντελεστή δυσκαμψίας των κολονών ίσο με k=6, (iv) με τη δυσκαμψία των δοκών και κολονών να προκύπτει από την ελαστική επίλυση του φορέα.  Εικόνα 5.4.5: Ο σκελετός και η προσομοίωση του μονώροφου χωρικού πλαισίου
Εικόνα 5.4.5: Ο σκελετός και η προσομοίωση του μονώροφου χωρικού πλαισίου Εικόνα 5.4.5: Ο σκελετός και η προσομοίωση του μονώροφου χωρικού πλαισίου Τα ονόματα, τα φορτία, οι συντεταγμένες και οι διαστάσεις των πλακών και των κολονών αναφέρονται στο σχήμα της §5.4.1, ενώ οι δοκοί έχουν διαστάσεις 250/500. Η ποιότητα σκυροδέματος είναι C30/37 (Ε=32.80 GPa). Επίλυση με το χέρι και με θεώρηση αφίπακτων κολονών (k=12) Η συγκεκριμένη επίλυση δόθηκε ως παράδειγμα σε όλες τις προηγούμενες παραγράφους του κεφαλαίου αυτού. Επίλυση με το excel και με θεώρηση αμφίπακτων κολονών (k=12) Αξιοποιείται το συνοδευτικό υπολογιστικό φύλλο ΄<diaphragm_ortho.xls> με τη θεώρηση άκαμπτων ζυγωμάτων. .jpg?bhow=0&w=500&h=500&Str=0) Εικόνα 5.4.5.2: Τα αποτελέσματα είναι ίδια με τις πράξεις στο χέρι.Ο φορέας σχεδιάζεται στο τέλος του φύλλου με την έλλειψη δυστρεψίας και με τις ισοδύναμες κολόνες.
Εικόνα 5.4.5.2: Τα αποτελέσματα είναι ίδια με τις πράξεις στο χέρι.Ο φορέας σχεδιάζεται στο τέλος του φύλλου με την έλλειψη δυστρεψίας και με τις ισοδύναμες κολόνες. Εικόνα 5.4.5.2: Τα αποτελέσματα είναι ίδια με τις πράξεις στο χέρι.Ο φορέας σχεδιάζεται στο τέλος του φύλλου με την έλλειψη δυστρεψίας και με τις ισοδύναμες κολόνες. Επίλυση με το excel και με θεώρηση κολονών με k=6 Από τα αποτελέσματα του excel προκύπτει ότι, το κέντρο ελαστικής στροφής, οι ακτίνες δυστρεψίας του φορέα και τα εντατικά μεγέθη είναι ακριβώς τα ίδια με τα αντίστοιχα μεγέθη των προηγούμενων περιπτώσεων. Το μόνο που αλλάζει είναι το μέγεθος των παραμορφώσεων , αλλά και πάλι οι σχετικές μεταξύ τους τιμές διατηρούνται σταθερές και ίσες με 12/6=2.00. Επίλυση με θεώρηση κανονικών ελαστικών δυσκαμψιών δοκών και κολονών Η επίλυση μπορεί να γίνει μόνο με τη χρήση λογισμικού. Πρόκειται για τη μελέτη <B_545>. Η θεωρία προσδιορισμού της διαφραγματικής λειτουργίας από τις αναλύσεις αναφέρεται αναλυτικά στο Παράρτημα Δ. 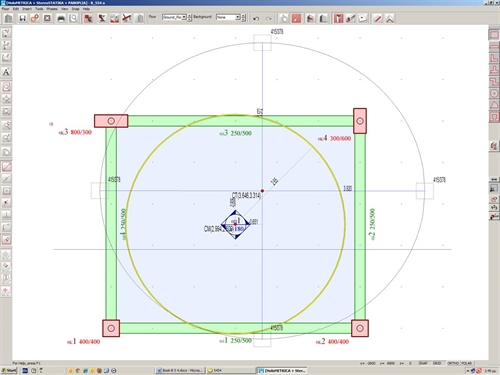 Εικόνα 5.4.5.4-1
Εικόνα 5.4.5.4-1 Εικόνα 5.4.5.4-1 Ο δακτύλιος αδράνειας είναι ίδιος με τις 2 προηγούμενες περιπτώσεις, καθώς εξαρτάται μόνο από τα φορτία, ενώ όλα τα υπόλοιπα μεγέθη προκύπτουν διαφορετικά, όπως αναμενόταν. Το κέντρο ελαστικής στροφής CTέχει συντεταγμένες (3.646, 3.314), ενώ οι ακτίνες δυστρεψίας ισούνται με rx=3.920 m και ry=3.572 m (;έναντι3.910 και 3.080 της θεώρησης αμφίπακτων κολονών). Οι ισοδύναμες κολόνες έχουν διατομή 415/378 (έναντι 524/406). Επιλέγω “Εμφάνιση”, “Αποτελέσματα διαφραγμάτων”, “εκτυπώσεις” και εμφανίζονται αναλυτικά όλα τα αποτελέσματα, τα οποία παρατίθενται στη συνέχεια μαζί με τα αντίστοιχα αποτελέσματα 1ης και 2ης περίπτωσης της θεώρησης αμφίπακτων κολονών σε παρένθεση. Σεισμός κατά X: θXZ= 4.3186·10-5 (4.765·10-5) mm, δXXo=0.6840 (0.3375) mm, δXYo=0.0 (0.0) mm Σεισμός κατά Y: θYZ=-3.4940·10-5 (-3.345·10-5) mm, δYXo=0.0 (0.0) mm, δYYo=0.8239 (0.5420) mm |  Εικόνα 5.4.5.4-2
Εικόνα 5.4.5.4-2 Εικόνα 5.4.5.4-2 |  Εικόνα 5.4.5.4-3
Εικόνα 5.4.5.4-3 Εικόνα 5.4.5.4-3 |  Εικόνα 5.4.5.4-4
Εικόνα 5.4.5.4-4 Εικόνα 5.4.5.4-4 | | | Δέσμευση στροφής
διαφράγματος | (1η Φ) μείον(2η Φόρτιση): | 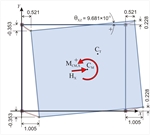 Εικόνα 5.4.5.4-5
Εικόνα 5.4.5.4-5 Εικόνα 5.4.5.4-5 | 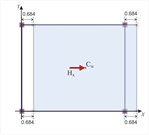 Εικόνα 5.4.5.4-6
Εικόνα 5.4.5.4-6 Εικόνα 5.4.5.4-6 | 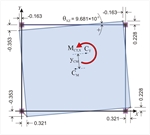 Εικόνα 5.4.5.4-7
Εικόνα 5.4.5.4-7 Εικόνα 5.4.5.4-7 | Οι μετατοπίσεις κάθε σημείου iδX,i , δY,i και η ενιάια γωνία στροφής του
διαφράγματος | Κάθε σημείο του διαφράγματος (άρα και το CT και το ) έχει τις ίδιες κύριες μετακινήσεις/em> | Το διάφραγμα εμφανίζει μόνο στροφή θXZ ως προς το CT. Οι μετακινήσεις λόγω στροφής κάθε σημείου i ισούνται με: δXt,i=δX,i-δXXo, δYt,i=δY,i-δXYo . |
Υπολογισμός διαφραγματικής λειτουργίας (συνέχεια)1ης(και μοναδικής) στάθμης  Εικόνα 5.4.5.4-8
Εικόνα 5.4.5.4-8 Εικόνα 5.4.5.4-8 | 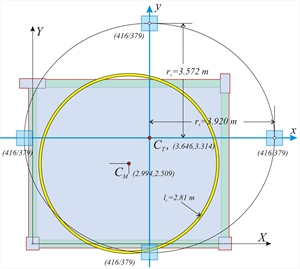 Εικόνα 5.4.5.4-10
Εικόνα 5.4.5.4-10 Εικόνα 5.4.5.4-10 | δέσμευση στροφής διαφράγματος |  Εικόνα 5.4.5.4-9
Εικόνα 5.4.5.4-9 Εικόνα 5.4.5.4-9 | Το διάφραγμα δε στρέφεται, αλλά κινείται μόνο παράλληλα προς τους άξονες X,Y. Κάθε σημείο του διαφράγματος (επομένως και το CT) έχει τις ίδιες κύριες μετακινήσεις: Η 3 η επίλυση ολοκληρώνονται οι αναγκαίες επιλύσεις για τον προσδιορισμό όλων των στοιχείων του διαφράγματος. | tan(2a)=2δXYo/(δXXo-δYYo)=0.0 à 2a=0° à a=0° Kxx=Hx/δxxo=90.6·103m/0.684·10-3m=132.5·106 N/m Kyy=Hy/δyyo=90.6·103m/0.824·10-3m=110.0·106 N/m MCT,X=90.6·yCM+90.6·cY=90.6·(3.316-2.500)+90.6·1.0=164.5 kNm Kθ=MCT,X/θXZ=164.5/9.681·10-5=17.0·105kNm rx=√Kθ/Kyy=√17.0·108N/m/110.0·106N/m=3.931m ry=√Kθ/Kxx=√17.0·108N/m/132.5·106N/m=3.582 m |
|