|
« Διαφραγματική λειτουργία
Κέντρο ελαστικής στροφής και ελαστικές μετακινήσεις διαφράγματος »
|
Κέντρο μάζας και ακτίνα αδράνειας Η αδρανειακή συμπεριφορά της μάζας Σ(mi) ενός διαφράγματος περιγράφεται από την αδρανειακά ισοδύναμη κατανομή της μάζας σε ένα δακτύλιο με συνολική μάζα Σ (mi), ο οποίος έχει ως κέντρο το Κέντρο μάζας CM και ως ακτίνα την Ακτίνα Αδράνειας ls. 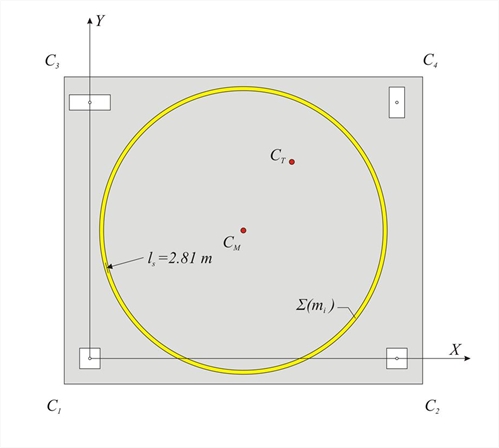 Εικόνα 5.4.2: Το κέντρο μάζας CM και ο ισοδύναμος δακτύλιος αδράνειας της μάζας με ακτίνα ls
Εικόνα 5.4.2: Το κέντρο μάζας CM και ο ισοδύναμος δακτύλιος αδράνειας της μάζας με ακτίνα ls Εικόνα 5.4.2: Το κέντρο μάζας CM και ο ισοδύναμος δακτύλιος αδράνειας της μάζας με ακτίνα ls Οι συντεταγμένες του κέντρου μάζας CMενός διαφράγματος με πολλές μάζες σημειακές είτε γραμμικά κατανεμημένες είτε επιφανειακές κατανεμημένες γραμμικά, προκύπτουν από τις σχέσεις:: Η ακτίνα αδράνειας ls του διαφράγματος ως προς το κέντρο μάζας CM ισούται με: όπου Χi και Υi είναι οι συντεταγμένες του κέντρου κάθε μάζας mi του διαγράμματος , ενώ Ipi είναι η πολική ροπή αδράνειας κάθε μάζας mi ως προς το κέντρο μάζας CM. Υπενθυμίζεται από τη μηχανική των υλικών ότι, ανάλογα με τον τρόπο διανομής μιας μάζας m, της οποίας το κέντρο απέχει απόσταση L από το κέντρο μάζας CM του διαφράγματος, η πολική ροπή αδράνειας ισούται με: - Για σημειακή μάζα: Ip=m·L2
- Για γραμμικά διανεμημένη μάζα σε μήκος l: Ip=m· (l2/12 + L2)
- Για επιφανειακά διανεμημένη μάζα σε ορθογώνιο διαστάσεων b,l: Ip=m· [(b2+l2)/12 + L2]
- Για επιφανειακά διανεμημένη μάζα σε τρίγωνο ή κυκλικό τμήμα: υπολογίζεται η ισοδύναμη κύρια ροπή αδράνειας ως προς το κέντρο μάζας του συγκεκριμένου τμήματος και προστίθεται ο όρος m·L2 του Steiner term.
Σε μεγάλες κατόψεις, η ακτίνα αδράνειας υπολογίζεται μόνο από τις αντιδράσεις των δοκών επί των κολονών του ορόφου, ενώ στην περίπτωση που τα επιμέρους γραμμικά φορτία ( π.χ. των τοίχων) είναι διανεμημένα ομοιόμορφα σε όλη την κάτοψη, η ακτίνα αδράνειας υπολογίζεται από τον τύπο όπυ L x, L y είναι οι διαστάσεις της κάτοψης. Ακτίνα αδράνειας : [g=10 m/sec2,οπότε δύναμη F=1 kN αντιστοιχεί σε μάζα m=0.1 t.] Πλάκα: m1=6.0m ·5.0m·0.71t/m2=21.3 t b1=6.0 m, l1=5.0 m, L1=0.0 m → Ip1=21.3t ·(6.02+5.02)m2/12=108.3 t·m2 Δοκός μεταξύ C1-C2: m2=6m·1.0t/m=6.0 t, l2=6.0 m, L2=2.5 m → Ip2=6.0· (62/12+2.52)=55.5 t·m2 Δοκός μεταξύ C3-C4: likewise m3=6.0 t, Ip2=55.5 t·m2 Δοκός μεταξύ C1-C3: m4=5.0m·1.0t/m=5.0 t, l4=5.0 m, L4=3.0 m → Ip4=5.0· (5.02/12+3.02)=55.4 t·m2 Δοκός μεταξύ C2-C4 likewise m5=5.0 t, Ip5=55.4 t · m2 Υποστυλώματα: m6=0.1 ·(4.00+4.00+6.0+4.5)=1.85 t, L6=√ (3.02+2.52)=3.905 m → Ip6=1.85 ·3.9052=28.2 t·m2.
|
« Διαφραγματική λειτουργία
Κέντρο ελαστικής στροφής και ελαστικές μετακινήσεις διαφράγματος »
|

|