|
« Προσομοίωση σκελετού
Επιλύσεις πλαισίων »
|
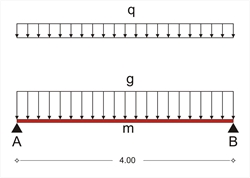 Εικόνα 3.3.2: Το ισοδύναμο αμφιαρθρωτό μέ-λος
Εικόνα 3.3.2: Το ισοδύναμο αμφιαρθρωτό μέ-λος
Εικόνα 3.3.2: Το ισοδύναμο αμφιαρθρωτό μέ-λος
Στο συγκεκριμένο παράδειγμα, η πλάκα s1 είναι αμφιαρθρωτή πάχους h=170 mm, με άνοιγμα l=4.00 m.Τα εντατικά μεγέθη σχεδιασμού προκύπτουν από το ίδιο βάρος της πλάκας, από το φορτίο επικάλυψης της πλάκας και το κινητό (ωφέλιμο) φορτίο q=5.00 kN/m2. Επειδή ο φορέας είναι πλάκα, λαμβάνεται για την επίλυση λωρίδα πλάτους 1.00 m. Το ίδιο βάρος του σκυροδέματος είναι 25.0 kN/m3οπότε: Ίδιο βάρος go=0.17mx1.00mx25.00kN/m3 =4.25 kN/m Επικάλυψη: ge=1.00mx1.00kN/m2 =1.00 kN/m Σύνολο μονίμων: g =5.25 kN/m Σύνολο ωφέλιμων: q=1.00mx5.00kN/m2 =5.00 kN/m Ο συνδυασμός σχεδιασμού που δίνει την οριακή κατάσταση αστοχίας προκύπτει από το φορτίο σχεδιασμού psd=γgx g+γqxq που στην προκειμένη περίπτωση είναι: psd=1.35g+1.50q=1.35x5.25+1.50x5.0=14.59 kN/m, οπότε τα εντατικά μεγέθη σχεδιασμού, με τα οποία θα διαστασιολογηθεί ο φορέας, προκύπτουν από τις σχέσεις: V Ad =-V Bd =14.59x(4.00/2)=29.18 kN M md =14.59x(4.002/8)=29.18 kNm
|
« Προσομοίωση σκελετού
Επιλύσεις πλαισίων »
|

|