Επιλύονται δύο παραδείγματα με τη γενική μέθοδο στον ίδιο απλό φορέα του Παραρτήματος Γ.1. Η επιλογή απλού φορέα είναι χρήσιμη για την άνετη παρακολούθηση των αποτελεσμάτων και την κατανόηση των θεμάτων του διαφραγματικού ορόφου. Η μελέτη είναι το μονόροφο <B_d9-1> για το οποίο με τη χρήση του συνοδευτικού λογισμικού, ή οποιουδήποτε άλλου λογισμικού, για κάθε μία από τις 3 φορτίσεις, υπολογίζουμε τις 2 μετατοπίσεις της κολόναςC1 που αντιστοιχούν στον κόμβο 5 και τη στροφή θXZ του διαφράγματος. Προαιρετικά, μπορούμε να υπολογίσουμε και τις μετατοπίσεις των υπόλοιπων σημείων του διαφράγματος. Με αυτές τις παραμορφώσεις υπολογίζονται όλα τα στοιχεία του διαφράγματος.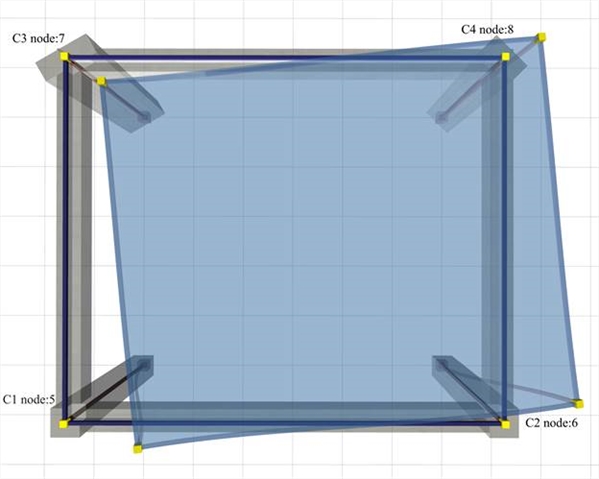 
Εικόνα Δ.7.1-1: Η απλή μελέτη με τις 4 κολόνες C1:400/400, C2:400/400, C3:800/300 φ=30º, C4:300/600 φ=45º, h=3.0 m, δοκοί 250/500 Εικόνα Δ.7.1-1: Η απλή μελέτη με τις 4 κολόνες C1:400/400, C2:400/400, C3:800/300 φ=30º, C4:300/600 φ=45º, h=3.0 m, δοκοί 250/500 Με την είσοδο στον “Όροφο”, καλούνται τα “Εργαλεία”, “Διαφραγματική επίλυση”, δίνουμε H=90.6 kN, cY=1.0 m, “Αμφίπακτα υποστυλώματα=OFF [*] Note Αν τεθεί “fixed columns=ON” τότε τα αποτελέσματα αντιστοιχούν στην παραδοχή αμφίπακτων κολονών και δίνει αποτελέσματα ίδια με των 2 πρώτων περιπτώσεων (ΕΝ: δεν το καταλαβαίνω). Οι μικρές διαφορές στα αποτελέσματα σε σχέση με τη δουλειά στο χέρι, αλλά και με το αρχείο .xlsοφείλονται στις μικρές διαφορές του κέντρου μάζας, λόγω των άνισων φορτίων του ίδιου βάρους των κολονών. ” , “ΟΚ”. Αμέσως εμφανίζεται η οθόνη με το δακτύλιο αδράνειας, το κέντρο ελαστικής στροφής, την έλλειψη δυστρεψίας και τον ισοδύναμο φορέα με τις 4 κολόνες. 
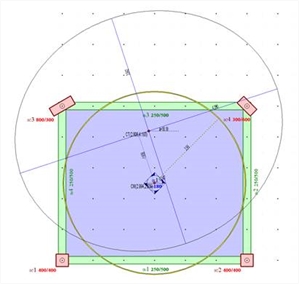Εικόνα Δ.7.1-2: Η εικόνα του output του λογισμικού Εικόνα Δ.7.1-2: Η εικόνα του output του λογισμικού
Ο δακτύλιος αδράνειας είναι ίδιος με τη προηγούμενη περίπτωση, δεδομένου ότι εξαρτάται μόνο από τα φορτία, όλα ωστόσο τα υπόλοιπα μεγέθη είναιδιαφορετικά, όπως αναμενόταν . Το κέντρο ελαστικής στροφής CT έχει συντεταγμένες (2.806, 4.193), και οι ακτίνες δυστρεψίας είναι rx=4.390 m, ry=3.842 m (έναντι συντεταγμένων 2.688, 4.897, rx=4.411 και ry=3.381 που έδωσε η θεώρηση αμφίπακτων κολονών) στο παράρτημα Γ. Καλώντας “Εμφάνιση” και μετά “Αποτελέσματα διαφραγμάτων”, “εκτυπώσεις”, εμφανίζονται αναλυτικά όλα τα αποτελέσματα μεθXZ =11.952×10-5. Εικόνα Δ.7.1-2: Η εικόνα του output του λογισμικού Τα υπόλοιπα αποτελέσματα είναι πιο πρακτικό να τα δούμε σε 3D καλώντας “Εμφάνιση”, “Αποτελέσματα διαφραγμάτων”, “3Dδιαφράγματος” και “ανάλυση με ελεύθερη στροφή” ή “ανάλυση με δεσμευμένη στροφή” ή “με στροφή μόνο”, όπως φαίνονται στις δύο επόμενες σελίδες. - Στο συγκεκριμένο παράδειγμα, επειδή είναι μονώροφο, η κατάσταση με στροφή μόνο είναι δυνατόν να προκύψει κατ’ ευθείαν από την ανάλυση, εφόσον βάλουμε ως εξωτερική φόρτιση μόνο ροπή. Αυτό οφείλεται στο γεγονός ότι το κέντρο ελαστικής στροφής CT στα μονώροφα διαφράγματα παραμένει, εξ’ ορισμού, ακίνητο ως προς το έδαφος.
Υπολογισμός [*]NoteΟι υπολογισμοί του διαφραγματικού ορόφου γίνονται αυτόματα από το λογισμικό. Εδώ βλέπουμε την επιβεβαίωση των αλγορίθμων που γίνεται με τα εργαλεία που προσφέρει το ίδιο το λογισμικό. διαφραγματικής λειτουργίας 
Εικόνα Δ.7.1-3 Εικόνα Δ.7.1-3 | 
Εικόνα Δ.7.1-4 Εικόνα Δ.7.1-4 | 
Εικόνα Δ.7.1-5 Εικόνα Δ.7.1-5 | | | 2η Φόρτιση : HX =90.6 kN και δέσμευση της στροφής του διαφράγματος | 3η Φόρτιση : HY =90.6 kN και δέσμευση της στροφής του διαφράγματος | 
Εικόνα Δ.7.1-6 Εικόνα Δ.7.1-6 | 
Εικόνα Δ.7.1-7 Εικόνα Δ.7.1-7 | 
Εικόνα Δ.7.1-8 Εικόνα Δ.7.1-8 | | Αποτελέσματα ανάλυσης: Οι μετακινήσεις του σημείου 1 είναι δ XX 1 =1.178, δ XY 1 =-0.395 mm και η ενιαία γωνία στροφής του διαφράγματος
θ XZ =11.952 ×10-5 | Αποτελέσματα ανάλυσης: Το διάφραγμα δε στρέφεται, γι’ αυτό κινείται μόνο παράλληλα προς τους άξονες X , Y . Άρα κάθε σημείο του διαφράγματος (επομένως και το CT ) έχει τις ίδιες κύριες μετακινήσεις: δ XXo =0.677 mm , δ XYo =-0.060. | Αποτελέσματα ανάλυσης: Το διάφραγμα δε στρέφεται και οι δύο παράλληλες μετακινήσεις του είναι: δ YXo =-0.0600, δ YYo =0.839 mm
Η γωνία του κυρίου συστήματος προκύπτει από τη σχέση:
tan (2 a )=2δ XYo /(δΧΧο-δ YYo )=
=2 ×(-0.060)/(0.677-0.839)= =0.741 → 2a=36.5° → a=18.2° |
Υπολογισμός διαφραγματικής λειτουργίας (συνέχεια) 
Εικόνα Δ.7.1-9 Εικόνα Δ.7.1-9 |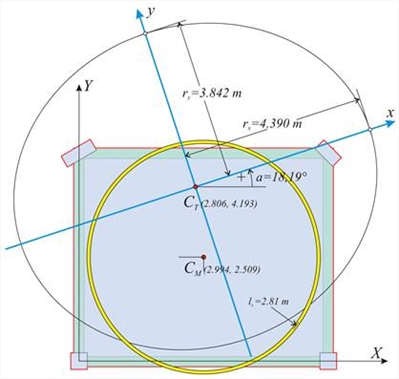 
Εικόνα Δ.7.1-10 Εικόνα Δ.7.1-10 | | 1η φόρτιση μείον 2η φόρτιση: HX=0, MXCT=90.6 × (YCT- YCM ) +90.6 |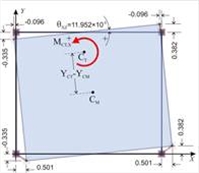 
Εικόνα Δ.7.1-11 Εικόνα Δ.7.1-11 | | Αποτελέσματα της αφαίρεσης: Το διάφραγμα έχει μόνο στροφή θ XZ με κέντρο τον πόλο περιστροφής CT . Οι μετακινήσεις του πρώτου σημείου λόγω στροφής: δ Xt ,1 =δ X ,1 -δ XXo =1.178-0.677 =0.501 mm ,
δ Yt ,1 = δ Y ,1 -δ XYo =-0.395+0.060 =-0.335 mm και XCT = X 1 -δ Yt ,1 /θ XZ = =0.0+0.335 ×10-3 /11.952 ×10-5 =2.803 m YCT = Y 1 +δ Xt ,1 /θ XZ = 0.0+0.501 ×10-3 /11.952 ×10-5 =4.192 m | Προσδιορισμός δυσκαμψιών και ακτίνων δυστρεψίας : Οι δυσκαμψίες Kxx, Kyy θα υπολογιστούν από τις εξισώσεις Γ.9.2 και Γ.9.3 της §Γ.9, με a=18.186° και tana=0.329:
Kxx=H/(δXXo+δXYo×tana)=[90.6/(0.677-0.060×0.329)]× 106N/m=
= 137.8×106 N/m
Kyy=H/(δYYo-XYo×tana)=[90.6/(0.839+0.060×0.329)]×10 6N/m=
=105.5×106 N/m MXCT [*]NoteΗ ροπή, η στροφή και η δυστρεψία Kθ είναι μεγέθη που είναι ίδια τόσο στο αρχικό σύστημα X0Y, όσο και στο κύριο σύστημα xCTy. Είναι προτιμότερο η εργασία να γίνεται στο αρχικό σύστημα, επειδή είναι πιο απλές οι πράξεις. =90.6 × ( Υ CT - YCM )+90.6 × cY =90.6 ×(4.193-2.509)+90.6×1.0=
=243.2 kNm ,
K θ = MXCT /θ XZ =243.2/11.952 ×10-5=20.3×105 kNm
rx =√ K θ / Kyy =√[20.3×108 Nm /105.5×106 N / m ]=4.39 m
ry =√ K θ / Kxx =√[20.3×108 Nm /137.8×106 N / m ]=3.84 m | - Οι σχέσεις που προσδιορίζουν τις συντεταγμένες του CT είναι γενικές και ισχύουν για κάθε σημείο του διαφράγματος. Για παράδειγμα, από την κολόνα 4 προκύπτουν:
XCT=X4-δYt,4/θXZ=6.0-0.382×10-3m/11.952×10-5=6.0-3.20=2.80 m YCT=Y4+δXt,4/θXZ=5.0-0.096×10-3m/11.952×10-5=5.0-0.80=4.20 m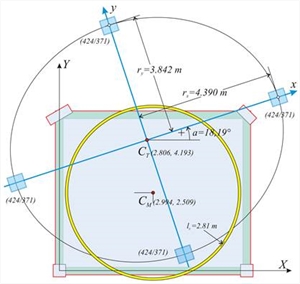 
Εικόνα Δ.7.1-12: Το ισοδύναμο σύστημα με 4 κολόνες διατομής 424/371 (στο “Ισοδύναμο σύστημα” δίνουμε k=1 → n=4k=4) Εικόνα Δ.7.1-12: Το ισοδύναμο σύστημα με 4 κολόνες διατομής 424/371 (στο “Ισοδύναμο σύστημα” δίνουμε k=1 → n=4k=4) | Στο συγκεκριμένο παράδειγμα, επειδή ο φορέας είναι μονώροφος (όπως και στον ισόγειο όροφο κάθε πολυώροφου κτιρίου), το ισοδύναμο σύστημα έχει την ίδια έλλειψη κατανομής της δυστρεψίας με την έλλειψη δυστρεψίας του πραγματικού ορόφου. Το λογισμικό, εφόσον επιλέξουμε “Ισοδύναμο σύστημα/σχεδ.”=ON, επιστρέφει την έλλειψη δυστρεψίας που επιβεβαιώσαμε αμέσως πιο πάνω με τις 4 ισοδύναμες κολόνες διατομής 424/373 επί των 4 κορυφών της έλλειψης, όπως φαίνεται στο σχήμα δίπλα. Ελέγχουμε την ισοδυναμία αυτών των 4 αμφίπακτων κολονών: | Εργαζόμαστε στο κύριο σύστημα συντεταγμένων, όπου η δυσκαμψία κάθε κολόνας στο τοπικό της σύστημα, συμπίπτει με το κύριο. Είναι Kx=12Ε×Ιx/h3 και Kx =12Ε×Ιy/h3 (βλέπε §5.1.1), δεδομένου ότι στο συγκεκριμένο παράδειγμα είχαμε επιλέξει ΟΧΙ επιρροή της διάτμησης, που ούτως ή άλλως είναι μικρή, επομένως kva=1. Ix = 0.373×0.4243/12= 23.693 ×10-4 m 4 , Iy = 0.424 ×0.3733/12=18.336×10-4 m 4 Με δεδομένα τα E=32.8 GP και h=3.0 m → Kx=12×32.8×109Pa×23.693×10-4m4/3.03m3 =34.54×106 N/m Ky =12 × 32.8 × 109 Pa × 18.336 × 10-4 m 4 /3.03 m 3 =26.73×106 N / m Επειδή οι ισοδύναμες κολόνες είναι 4 → Kxx=Σ(Kx)=4×34.54=138.2×106 N /m, Kyy =Σ( Ky )=4×26.73=106.9×106 N / m , δηλαδή όση και η πραγματική δυσκαμψία (μικροδιαφορές δικαιολογούνται από την ανάγκη χρήσης ακέραιων mm). Η δυσκαμψία του ισοδύναμου διαφράγματος είναι Kθ=Σ(Kxi×yi2+Kyi×xi2+0.0) (εξίσωση 7, §Γ.5) → Kθ=2×Κx×3.8422+2×Ky×4.3902=2×34.54×106N/m×14.76m2 + 2×26.73×106N/m×19.271m 2= (10.2+10.3)×105 kNm =20.5×105 kNm , δηλαδή όση και η πραγματική δυστρεψία. Είναι προφανές ότι και οι τιμές των rx, ry θα είναι ίδιες, δεδομένου ότι αποτελούν τηντετραγωνική ρίζα του λόγου ίσων ποσοτήτωνrxΖ=√(Kθ/Kyy)=4.39 m, ryΖ=√(Kθ /Kxx)=3.84 m. Το ισοδύναμο κτίριο μπορεί να έχει 4 κολόνες μόνο, ή οποιοδήποτε πλήθος κολονών n=4k, όπου κ ακέραιος αριθμός διάφορος του μηδενός, π.χ. 4, 8, 12, 16, 20, … Οι κολόνες αυτές ανά 4 τοποθετούνται συμμετρικά ως προς το κέντρο ελαστικής στροφής. Για παράδειγμα, η περίπτωση των 8 κολονών με διατομή 356/312, δίνει: Ix = 0.312×0.3563/12= 11.731 ×10-4 m 4 , Iy = 0.356 ×0.3123/12=9.010×10-4 m 4 Με δεδομένα τα E=32.8 GP και h=3.0 m → Kx=12×32.8×109Pa×11.731×10-4m4/3.03m3=17.01×106 N/m, Ky=12×32.8×109Pa×9.010×10-4m4/3.03m3=13.13×106 N/m. Επειδή οι ισοδύναμες κολόνες είναι 8 → Kxx=Σ(Kx)=8×17.01=136.8×106 N/m και Kyy= Σ(Ky)=8×13.13=105.1×106 N /m. Για να υπολογίσουμε τη δυστρεψία, λαμβάνουμε τις συντεταγμένες των 4 ενδιάμεσων σημείων τα οποία δίνονται στην οθόνη και στις “εκτυπώσεις” (εφόσον ζητήσουμε “coords”) και είναι κατά x και y, ±3.105 m και ±2.717 m αντίστοιχα. Εναλλακτικοί ισοδύναμοι φορείς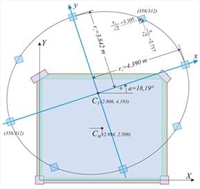 
Εικόνα Δ.7.1-13: Περίπτωση 8 κολονών (k=2, n=4k=8) Ισοδύναμης διατομής 356/312 Εικόνα Δ.7.1-13: Περίπτωση 8 κολονών (k=2, n=4k=8) Ισοδύναμης διατομής 356/312 |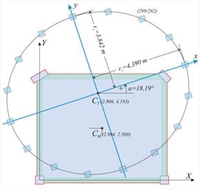 
Εικόνα Δ.7.1-14: Περίπτωση 16 κολονών (k=4, n=4k=16) Ισοδύναμης διατομής 299/262 Εικόνα Δ.7.1-14: Περίπτωση 16 κολονών (k=4, n=4k=16) Ισοδύναμης διατομής 299/262 | | | |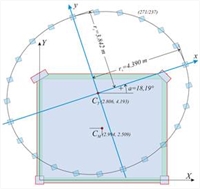 
Εικόνα Δ.7.1-15: Περίπτωση 24 κολονών (k=6, n=4k=24) Ισοδύναμης διατομής 271/237 Εικόνα Δ.7.1-15: Περίπτωση 24 κολονών (k=6, n=4k=24) Ισοδύναμης διατομής 271/237 |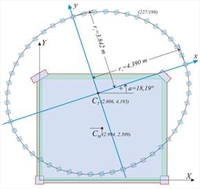 
Εικόνα Δ.7.1-16: Περίπτωση 48 κολονών (k=12, n=4k=48) Ισοδύναμης διατομής 227/199 Εικόνα Δ.7.1-16: Περίπτωση 48 κολονών (k=12, n=4k=48) Ισοδύναμης διατομής 227/199 | | | | K θ =Σ( Kxi × yi 2 + Kyi × xi 2 )= 2 × Κ x × 3.8422+4 × Κ x × 2.717 2 +2 × Ky × 4.3902+4 × Ky × 3.1052= =[17.01 ×(29.52+29.53)+13.13×(38.54+38.56)]×103 kNM =[10.1+10.1]×105 kNM =20.2×105 kNM Δηλαδή και το σύστημα των 8 αμφίπακτων κολονών είναι ισοδύναμο με τον πραγματικό φορέα. Με τον ίδιο τρόπο επαληθεύεται ότι όλα τα συστήματα n=4k είναι ισοδύναμα με το αρχικό.
Η μελέτη είναι το τριώροφο <B_d9-2> και με τη χρήση του συνοδευτικού λογισμικού ή οποιουδήποτε άλλου λογισμικού, σε κάθε στάθμη χωριστά και στο συγκεκριμένο παράδειγμα, στη 2η στάθμη για κάθε μία από τις 3 φορτίσεις, υπολογίζουμε τις 2 μετατοπίσεις της C1 που αντιστοιχούν στον κόμβο 9 και τη στροφή θXZ του διαφράγματος. Προαιρετικά, θα μπορούσαμε να υπολογίσουμε και τις μετατοπίσεις των υπόλοιπων σημείων του διαφράγματος. Με αυτές τις παραμορφώσεις υπολογίζονται όλα τα στοιχεία του διαφράγματος.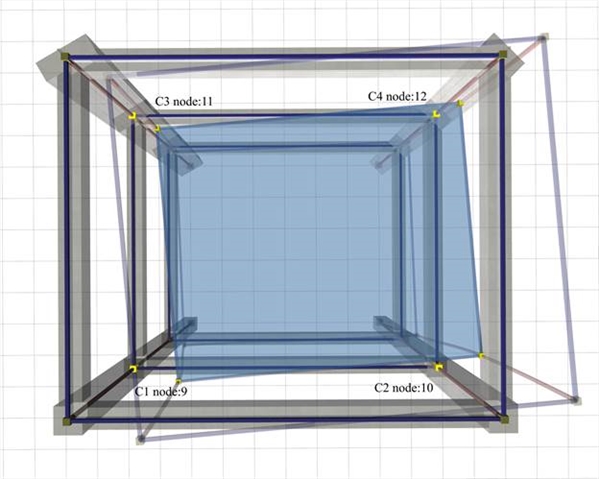 
Εικόνα Δ.7.2-1: Η απλή μελέτη με τους 3 ορόφους και τις 4 κολόνες. Ο όροφος είναι τυπικός, ίδιος με τον όροφο του 1ου παραδείγματος Εικόνα Δ.7.2-1: Η απλή μελέτη με τους 3 ορόφους και τις 4 κολόνες. Ο όροφος είναι τυπικός, ίδιος με τον όροφο του 1ου παραδείγματος
Με την είσοδο στον “Όροφο”, καλούνται τα “Εργαλεία”, “Διαφραγματική επίλυση”, δίνουμε H=90.6 kN, cy =1.0 m, “Αμφίπακτα υποστυλώματα=OFF” , “ΟΚ”. Τότε εμφανίζονται στην οθόνη τα στοιχεία του διαφράγματος του ορόφου στον οποίο βρισκόμαστε. Μεταβαίνουμε στον 1ο όροφο που αντιστοιχεί στη δεύτερη στάθμη του κτιρίου.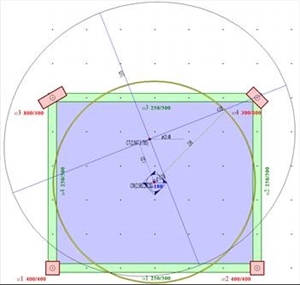 
Εικόνα Δ.7.2-2: Η εικόνα του output του λογισμικού Εικόνα Δ.7.2-2: Η εικόνα του output του λογισμικού Καλώντας “Εμφάνιση” και μετά “Αποτελέσματα διαφραγμάτων”, “εκτυπώσεις”, εμφανίζονται αναλυτικά τα αποτελέσματα για όλες τις στάθμες. Στη 2η στάθμη είναι θXZ=30.2962×10-5. Τα υπόλοιπα αποτελέσματα φαίνονται καλύτερα σε 3D καλώντας “Εμφάνιση”, “Αποτελέσματα διαφραγμάτων”, “3D διαφράγματος” και “ανάλυση με ελεύθερη στροφή” ή “ανάλυση με δεσμευμένη στροφή” ή “με στροφή μόνο”, όπως παρουσιάζονται στις δύο επόμενες σελίδες. Εικόνα Δ.7.2-2: Η εικόνα του output του λογισμικού - Στο συγκεκριμένο παράδειγμα, επειδή είναι πολυώροφο, η κατάσταση ενός διαφράγματος με στροφή μόνο, δηλαδή με το σημείο CT ακίνητο ως προς το έδαφος, μπορεί να προκύψει μόνο με το τέχνασμα της γενικής μεθόδου που ακολουθείται .
Υπολογισμός [*]Note Οι υπολογισμοί του διαφραγματικού ορόφου γίνονται αυτόματα από το λογισμικό. Εδώ βλέπουμε την επιβεβαίωση των αλγορίθμων που γίνεται με τα εργαλεία που προσφέρει το ίδιο το λογισμικό. 
Εικόνα Δ.7.2-3 Εικόνα Δ.7.2-3 | 
Εικόνα Δ.7.2-4 Εικόνα Δ.7.2-4 | 
Εικόνα Δ.7.2-5 Εικόνα Δ.7.2-5 | | | 2η Φόρτιση : HX =90.6 kN
και δέσμευση της στροφής του διαφράγματος | 3η Φόρτιση : HY =90.6 kN
και δέσμευση της στροφής του διαφράγματος |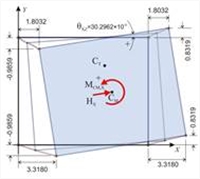 
Εικόνα Δ.7.2-6 Εικόνα Δ.7.2-6 | 
Εικόνα Δ.7.2-7 Εικόνα Δ.7.2-7 | 
Εικόνα Δ.7.2-8 Εικόνα Δ.7.2-8 | | Αποτελέσματα ανάλυσης: Οι μετακινήσεις του σημείου 1 είναι δ XX 1 =3.318, δ XY 1 =-0.986 mm και η ενιαία γωνία στροφής του διαφράγματος
θ XZ =30.2962 ×10-5 | Αποτελέσματα ανάλυσης: Το διάφραγμα δε στρέφεται, γι’ αυτό κινείται μόνο παράλληλα προς τους άξονες X , Y . Άρα κάθε σημείο του διαφράγματος (επομένως και το CT ) έχει τις ίδιες κύριες μετακινήσεις:
δ XXo =2.1712 mm , δ XYo =-0.1235 | Αποτελέσματα ανάλυσης: Το διάφραγμα δε στρέφεται και οι δύο παράλληλες μετακινήσεις του είναι:
δ YXo =-0.1235, δ YYo =2.4362 mm
Η γωνία του κυρίου συστήματος προκύπτει από τη σχέση:
tan (2 a )=2δ XYo /(δΧΧο-δ YYo )=
2 ×(-0.1235)/(2.1712-2.4362)= 0.932 → 2a=43.0° → a=21.5° |
Υπολογισμός διαφραγματικής λειτουργίας 2ης στάθμης (συνέχεια)
Εικόνα Δ.7.2-9 Εικόνα Δ.7.2-9 |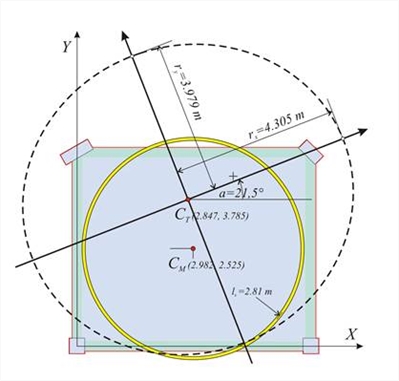 
Εικόνα Δ.7.2-10 Εικόνα Δ.7.2-10 | | 1η φόρτιση μείον 2η φόρτιση: HX =0, MXCT =90.6 × (YCT- YCM ) +90.6 | 
Εικόνα Δ.7.2-11 Εικόνα Δ.7.2-11 | | Αποτελέσματα της αφαίρεσης: Το διάφραγμα έχει μόνο στροφή θ XZ με κέντρο τον πόλο περιστροφής CT . Οι μετακινήσεις του πρώτου σημείου λόγω στροφής: δ Xt ,1 =δ X ,1 -δ XXo =
=3.3180-2.1712 =1.1468,
δ Yt ,1 = δ Y ,1 -δ XYo =
=-0.9859+0.1235 =-0.8624 και XCT = X 1 -δ Yt ,1 /θ XZ = 0.0+0.8624 ×10-3 /30.2962 ×10-5 =2.847 m YCT = Y 1 +δ Xt ,1 /θ XZ = 0.0+1.1468 ×10-3 /30.2962 ×10-5 =3.785 m | Προσδιορισμός δυσκαμψιών, ακτίνων δυστρεψίας και ισοδύναμου συστήματος : Οι δυσκαμψίες Kxx, Kyy θα υπολογιστούν από τις εξισώσεις Γ.9.2 και Γ.9.3 της §Γ.9 με a=21.49° → tana=0.393:
Kxx=H/(δXXo+δXYo×tana)= =[90.6/(2.1712-0.1235×0.393)]×106N/m= 42.7×106 N/m
Kyy=H/(δYYo-XYo×tana)= =[90.6/(2.4362+0.1235×0.393)]×106N/m= 36.5×106 N/m MXCT=90.6 × ( Υ CT -YCM)+90.6 × cY=90.6 ×(3.785-2.525)+90.6×1.0=
204.8 kNm,
K θ = MCT,X/ θ XZ =204.8/30.2962 ×10-5=6.759×105 kNm
rx=√K θ /Kyy=√[6.759×108Nm/36.5×106N/m]=4.30 m
ry=√K θ /Kxx=√[6.759×108Nm/42.7×106N/m]=3.98 m | - Οι σχέσεις που προσδιορίζουν τις συντεταγμένες του CT είναι γενικές και ισχύουν για κάθε σημείο του διαφράγματος. Για παράδειγμα, από την κολόνα 4 προκύπτουν:
XCT=X4-δYt,4/θXZ=6.0-0.9553×10-3m/30.2962×10-5=6.0-3.153=2.847 m YCT=Y4+δXt,4/θXZ=5.0-0.3681×10-3m/30.2962×10-5=5.0-1.215=3.785 m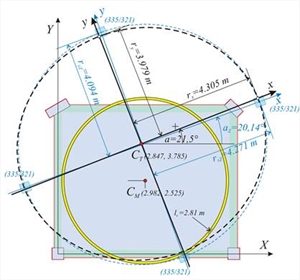 
Εικόνα Δ.7.2-12: Ισοδύναμο διάφραγμα 2ης στάθμης με 4 κολόνες διατομής 335/321 (στο “Ισοδύναμο σύστημα” δίνουμε k=1 → n=4k=4) Εικόνα Δ.7.2-12: Ισοδύναμο διάφραγμα 2ης στάθμης με 4 κολόνες διατομής 335/321 (στο “Ισοδύναμο σύστημα” δίνουμε k=1 → n=4k=4) | Το ισοδύναμο σύστημα του φορέα του τριώροφου κτιρίου, αποτελείται από 3 ισοδύναμα, προς τα πραγματικά, διαφράγματα του φορέα. Τα αποτελέσματα των πραγματικών διαφραγμάτων και των ισοδύναμων δίνονται στις “εκτυπώσεις” του λογισμικού. Από αυτή εκτυπώνουμε τους δύο πίνακες των ισοδύναμων διαφραγμάτων. | Παραμορφώσεις Ισοδύναμου Συστήματος | Στάθμη | dXXo,i
mm | dXYo,i
mm | qXZM,i
1.0e-5 | dYYo,i
mm | dXXoZ,i
mm | dXYoZ,i
mm | dYYoZ,i
mm | qXZMZ,i
1.0e-5 | | 1 | 0.612 | -0.079 | 4.2009 | 0.773 | 0.612 | -0.079 | 0.773 | 4.2009 | | 2 | 2.171 | -0.123 | 13.4045 | 2.436 | 1.559 | -0.044 | 1.663 | 9.2036 | | 3 | 4.198 | -0.072 | 24.6910 | 4.437 | 2.026 | 0.052 | 2.001 | 11.2865 | Διατομές Ισοδύναμου Συστήματος | Στάθμη | hi
m | αZ,i
deg | MXM,i
KNm | KqZ,i
MNm | KxxZ,i
MN/m | KyyZ,i
MN/m | rxZ,i
m | ryZ,i
m | AxZ,i
mm | AyZ,i
mm | | 1 | 3.00 | 22.3069 | 90.60 | 2156.7 | 156.30 | 112.45 | 4.379 | 3.715 | 441 | 374 | | 2 | 3.00 | 20.1371 | 90.60 | 984.4 | 58.72 | 53.95 | 4.271 | 4.094 | 335 | 321 | | 3 | 3.00 | 38.0593 | 90.60 | 802.7 | 43.83 | 46.21 | 4.168 | 4.279 | 306 | 314 | Επιβεβαίωση των αποτελεσμάτων που αναγράφονται στους πίνακες και προκύπτουν βάσει της θεωρίας που έχει αναπτυχθεί στην §Δ.6 : δ XXo Ζ,1 = δ XXo ,1 -0.0=0.612 , δ XYo Ζ,1 =δ XYo ,1 -0.0=-0.079, δ YYo Ζ,1 =δ YYo ,1 -0.0=0.773, θ XZ Μ Z ,1 = θ X ΖΜ,1 –0.0=4.2009 δ XXo Ζ,2 = δ XXo ,2 -δ XXo ,1 =2,171-0.612=1.559, δ XYo Ζ,2 =δ XYo ,2 -δ XYo ,1 =-0.123-(-0.079)=-0.044
δ YYo Ζ,2 =δ YYo ,2 -δ YYo ,1 =2.436-0.773=1.663, θ XZ Μ Z ,2 = θ X ΖΜ,2 –θ XZ Μ,1 =13.4045-4.2009=9.2036 δ XXo Ζ,3 = δ XXo ,3 -δ XXo ,2 =4.198-2.171= 2.026, δ XYo Ζ,3 =δ XYo ,3 -δ XYo ,2 =-0.072-(-0.123)=0.051
δ YYo Ζ,3 =δ YYo ,3 -δ YYo ,2 =4.437-2.436=2.001, θ XZ Μ Z ,3 = θ X ΖΜ,3 –θ XZ Μ,2 =24.6910-13.4045=11.2865 Από αυτά τα μεγέθη προκύπτουν τα διαφραγματικά στοιχεία για όλες τις στάθμες, οπότε συγκεκριμένα για τη 2η στάθμη είναι: tan (2 az ,2 )=2 × δ XYo Ζ,2 /( δ XXo Ζ,2 - δ YYo Ζ,2 )=2 × (-0.044)/(1.559-1.663) → tan(2az,2)=0.8462 → az ,2 =20.12º και tanaz ,2 =0.3667 K θ Z ,2 =ΜΧΜ,2/θ XZ Μ Z ,2 =90.6 ×1.0/ 9.2036=984.4, KxxZ ,2 = H /(δ XXoZ ,2 +δ XYoZ ,2 × tanaZ ,2 )=90.6/(1.559+(-0.044) × 0.3667)=58.7 και Kyy Ζ,2 = H /(δ YYoZ ,2 -δ XYoZ ,2 × tanaZ ,2 )=90.6/(1.663-(-0.044) ×0.3667)=53.95 rxZ ,2 =√ K θ Z ,2 / KyyZ ,2 =√(984.4/53.95)=4.27, ryZ ,2 =√ K θ Z ,2 / KxxZ ,2 =√(984.4/58.72)=4.094 όπερ έδει δείξαι.
|